Sekcje: Matematyka
Rodzaj lekcji:
Cel: tworzą zdolność do faktoryzacji wielomianu.
Zadania:
Metody pracy:
Wyposażenie lekcji: tablica interaktywna lub luneta, tabele ze skróconymi wzorami mnożenia, instrukcje, materiały do pracy grupowej.
Struktura lekcji:
Podczas zajęć
1. Moment organizacyjny
Nauczyciel sprawdza gotowość klasy i uczniów do lekcji.
2. Sformułowanie tematu, celów i zadań lekcji-praktyki
3. Sprawdzanie pracy domowej
Na tablicy znajdują się przykłady rozwiązywania zadań domowych nr 943 (a, c); nr 945 (c, d). Próbki zostały wykonane przez uczniów klasy. (Ta grupa uczniów została zidentyfikowana na poprzedniej lekcji, sformalizowali swoją decyzję na przerwie). Uczniowie przygotowują się do „obrony” rozwiązań.
Nauczyciel:
Sprawdza pracę domową w zeszytach uczniów.
Zachęca uczniów do odpowiedzi na pytanie: „Jakie trudności sprawiło zadanie?”.
Propozycje porównania ich rozwiązania z rozwiązaniem na tablicy.
Zachęca uczniów przy tablicy do odpowiedzi na pytania, które uczniowie mieli w terenie podczas sprawdzania próbek.
Komentuje odpowiedzi uczniów, uzupełnia odpowiedzi, wyjaśnia (w razie potrzeby).
Podsumowuje pracę domową.
Studenci:
Przedstaw pracę domową nauczycielowi.
Zmieniaj zeszyty (w parach) i sprawdzaj ze sobą.
Odpowiedz na pytania nauczyciela.
Sprawdź swoje rozwiązanie za pomocą próbek.
Działają jak przeciwnicy, dokonują uzupełnień, poprawek, zapisują inną metodę, jeśli metoda rozwiązania w zeszycie różni się od metody na tablicy.
Poproś o niezbędne wyjaśnienia uczniom, nauczycielowi.
Znajdź sposoby sprawdzenia wyników.
Weź udział w ocenie jakości zadań przy tablicy.
4. Aktualizacja podstawowej wiedzy i umiejętności uczniów
1. Praca ustna
Nauczyciel:
Odpowiedz na pytania:
2. Na tablicy zapisane są wielomiany:
1. 14x 3 - 14x 5
2. 16x 2 - (2 + x) 2
3. 9 - x 2 - 2xy - y 2
4.x3 - 3x - 2
Nauczyciel zaprasza uczniów do faktoryzacji wielomianów nr 1-3:
Jeden uczeń otrzymuje propozycję faktoryzacji wielomianu nr 4 (zadanie indywidualne o podwyższonym stopniu trudności, zadanie wykonywane na formacie A4). Następnie na tablicy pojawia się przykładowe rozwiązanie zadania nr 1-3 (wykonane przez nauczyciela), przykładowe rozwiązanie zadania nr 4 (wykonane przez ucznia).
3. Rozgrzej się
Nauczyciel daje instrukcje dotyczące faktoryzacji i wyboru litery związanej z poprawną odpowiedzią. Dodając litery otrzymasz nazwisko największego matematyka XVII wieku, który wniósł ogromny wkład w rozwój teorii rozwiązywania równań. (Kartezjusz)
5. Wychowanie fizyczne Uczniowie czytają wypowiedzi. Jeśli stwierdzenie jest prawdziwe, uczniowie powinni podnieść ręce do góry, a jeśli to nieprawda, usiąść przy biurku. (Załącznik 2)
6. Instrukcja wykonania zadań warsztatu.
Na tablicy interaktywnej lub osobnym plakacie stół z instrukcjami.
Podczas rozkładania wielomianu na czynniki należy przestrzegać następującej kolejności:
1. usuń wspólny czynnik z nawiasów (jeśli są);
2. stosować skrócone wzory mnożenia (jeśli to możliwe);
3. zastosować metodę grupowania;
4. sprawdź wynik uzyskany przez mnożenie.
Nauczyciel:
Oferuje instrukcje dla uczniów (podkreśla krok 4).
Oferuje realizację zadań warsztatowych w grupach.
Rozkłada arkusze pracy na grupy, arkusze z kalką do wypełniania zadań w zeszytach i ich późniejszej weryfikacji.
Wyznacza czas na pracę w grupach, na pracę w zeszytach.
studenci:
Przeczytali instrukcje.
Nauczyciele uważnie słuchają.
Siedzą w grupach (po 4-5 osób każda).
Przygotuj się do praktycznej pracy.
7. Wykonywanie zadań w grupach
Karty pracy z zadaniami dla grup. (Załącznik 3)
Nauczyciel:
Kieruje samodzielną pracą w grupach.
Ocenia zdolność studentów do samodzielnej pracy, umiejętność pracy w grupie, jakość projektu arkusza roboczego.
studenci:
Wykonuj zadania na arkuszach kalki zawartych w skoroszycie.
Omów racjonalne rozwiązania.
Przygotuj arkusz roboczy dla grupy.
Przygotuj się do obrony swojej pracy.
8. Sprawdzanie i omawianie zadania
Odpowiedzi na tablicy.
Nauczyciel:
Zbiera kopie decyzji.
Zarządza pracą uczniów raportujących na kartach pracy.
Proponuje przeprowadzenie samooceny swojej pracy, porównanie odpowiedzi w zeszytach, zeszytach i próbkach na tablicy.
Przypomina kryteria oceniania pracy, udziału w jej realizacji.
Zawiera wyjaśnienia dotyczące pojawiających się decyzji lub problemów z samooceną.
Podsumowuje pierwsze wyniki praktycznej pracy i refleksji.
Podsumowuje (wraz z uczniami) lekcję.
Mówi, że ostateczne wyniki zostaną zsumowane po sprawdzeniu kopii prac wykonanych przez uczniów.
studenci:
Daj kopie nauczycielowi.
Karty pracy są dołączone do tablicy.
Sprawozdawczość z wykonania pracy.
Dokonać samooceny i samooceny wykonania pracy.
9. Zadawanie pracy domowej
Praca domowa jest wypisana na tablicy: nr 1016 (a, b); 1017 (c, d); nr 1021 (d, e, f)*
Nauczyciel:
Proponuje spisanie obowiązkowej części zadania w domu.
Daje komentarz na temat jego realizacji.
Zaprasza bardziej przygotowanych uczniów do wpisania nr 1021 (d, e, f)*.
Informuje o przygotowaniu się do następnej lekcji powtórkowej
PLAN LEKCJI
Rodzaj lekcji : lekcja uczenia się nowego materiału w oparciu o uczenie problemowe9 Cel lekcji
stworzyć warunki do ćwiczenia umiejętności i umiejętności faktoryzacji wielomianu różnymi metodami.
10. Zadania:
Edukacyjny
powtórz algorytmy działań: wyjęcie wspólnego czynnika z nawiasu, metoda grupowania, skrócone wzory mnożenia.
umiejętności budowania:
– zastosować wiedzę na temat „faktoryzacja wielomianu na różne sposoby”;
– wykonywać zadania zgodnie z wybraną metodą działania;
– wybierz najbardziej racjonalny sposób racjonalizacji obliczeń, przekształcenia wielomianów.
Edukacyjny
promowanie rozwoju zdolności poznawczych, uwagi, pamięci, myślenia uczniów poprzez stosowanie różnych ćwiczeń;
rozwijać umiejętności samodzielnej pracy i pracy grupowej; utrzymuj zainteresowanie uczniów matematyką
wychowawcy
utrzymuj zainteresowanie uczniów matematyką
11. Kształt UUD
Osobisty: świadomość celu działania (oczekiwany rezultat), świadomość lub wybór metody działania (Jak to zrobię? Jak uzyskam wynik?), analiza i ocena wyniku; ocena ich możliwości;
Przepisy: uwzględniać zasadę w planowaniu i kontrolowaniu sposobu rozwiązywania, planowania, oceny wyników pracy;
Kognitywny: wybór najskuteczniejszych sposobów rozwiązywania problemów, strukturyzowanie wiedzy;konwertowanie informacji z jednej formy do drugiej.
Rozmowny: planowaniewspółpraca edukacyjna z nauczycielem i rówieśnikami, przestrzeganie zasad zachowania mowy, umiejętność wyrażania się iuzasadniają swój punkt widzenia, uwzględniają różne opinie i dążą do koordynowania różnych stanowisk we współpracy.
12. Metody:
według źródeł wiedzy: werbalnej, wizualnej;
dotyczące charakteru czynności poznawczych: reprodukcyjna, częściowo eksploracyjna.
13. Formy pracy studenta: frontalny, indywidualny, grupowy.
14. Niezbędny Wyposażenie techniczne: komputer, projektor, tablica interaktywna, materiały informacyjne (arkusz samokontroli, karty zadań), prezentacja elektroniczna wykonana w programiemocpunkt
15.Planowane wyniki :
Osobisty rozwijanie poczucia szacunku do samego siebie i wzajemnego; rozwój współpracy przy pracy w grupach;
Metapodmiot rozwój mowy; rozwój samodzielności uczniów; rozwój uwagi w poszukiwaniu błędów.
Przedmiot rozwój umiejętności pracy z informacją, opanowanie rozwiązań
Podczas zajęć:
1. Powitanie studentów. Sprawdzenie przez nauczyciela gotowości klasy do lekcji; organizacja uwagi; samouczek dotyczący arkusza ocenyZałącznik 1 , doprecyzowanie kryteriów oceny.
Sprawdzanie prac domowych i aktualizowanie wiedzy
1. 3a + 6b= 3(a + 2b)2. 100 - 20s + s 2 = (10 + s) 2
3. z 2 - 81 \u003d (s - 9) (s + 9)
4. 6x 3 – 5x 4 = x 4 (6x - 5)
5. a - 3 r - 4a + 12 \u003d r (a - 3) - 4 (a - 3)
6. 0,09x 2 - 0,25 lat 2 \u003d (0,03x - 0,05 roku) (0,03x + 0,05 roku)
7. c (x - 3) -d(x - 3) \u003d (x - 3) (s -d)
8. 14x 2 - 7x \u003d 7x (7x - 1)
9. -1600 + a 12 = (40 + a 6 ) (40 - a 6 )
10,9x 2 – 24xy + 16lat 2 = (3x - 4 lata) 2
11,8s 3 – 2s 2 + 4s - 1 =
2s 2 (4s - 1) + (4s - 1) = (4s - 1)2s 2
12. b 4 + z 2 – 2 b 2 c = (b – c) 2
(zadania domowe są pobierane z podręcznika, uwzględniają faktoryzację na różne sposoby. Aby wykonać tę pracę, uczniowie muszą pamiętać wcześniej przestudiowany materiał)
Odpowiedzi zapisane na slajdzie zawierają błędy, uczniowie uczą się widzieć sposoby, a także zauważając błędy, zapamiętywać sposoby działania,
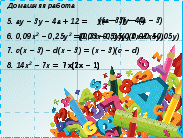

Uczniowie w grupach, po sprawdzeniu swojej pracy domowej, przyznają punkty za wykonaną pracę.
2 PrzekaźnikZałącznik 2 (członkowie zespołu na zmianę wykonują zadanie, a strzałka łączy przykład i sposób jego rozkładu)
3a-12b = 3(a – 4 b)2a + 2b + a 2 +ab = (+ b) (2 + a)
9a 2 – 16b 2 = ( 3a - 4 b)(3a + 4b)
16a 2 - 8ab+b 2 = (4a – b) 2
7a 2 b-14ab 2 + 7ab = 7ab(a - 2b + 1)
a 2 + ab- a - ac- bc + c = (a + b - 1) (a - c)
25a 2 + 70ab + 49b 2 = ( 5a + 7 b) 2
5x 2 - 45lat 2 \u003d 5 (x - 3 lata) (x + 3 lata)
![]()
Nie faktoryzuje
Metoda grupowania

Za pomocą slajdu sprawdza się wykonaną pracę i zwraca się uwagę na fakt, że ostatni przykład należy połączyć z dwiema metodami dekompozycji (w nawiasach dzielnik wspólny i skrócona formuła mnożenia)
Uczniowie oceniają wykonaną pracę, wpisują wyniki do arkuszy ocen, a także formułują temat lekcji.

3. Wykonywanie zadań (studenci są zaproszeni do wykonania zadania. Omawiając rozwiązanie w grupie, chłopaki dochodzą do wniosku, że potrzeba kilku sposobów na faktoryzację tych wielomianów. Zespół, który jako pierwszy oferuje prawidłowy rozkład, ma prawo do zapisania swoje rozwiązanie na tablicy, reszta spisuje je w zeszycie.. Zespół nawiązał pracę, aby pomóc uczniom, którzy mają trudności z poradzeniem sobie z zadaniem)
1) 2a 2 - 2b 25) 5m 2 + 5n 2 – 10min
9) 84 - 42 lata - 7xy + 14x
13) x 2 y+14xy 2 + 49 lat 3
2) 3a 2 + 6ab + 3b 2
6) cx 2 – cy 2
10) -7b 2 – 14bc – 7c 2
14) 3ab 2 – 27a
3) x 3 – 4x
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8a 3 b+56a 2 b 2 – 98ab 3
4) 3ab + 15b - 3a - 15
8) x 4 - x 2
12) c 4 - 81
16) 0 , 09t 4 - t 6
4. Etap końcowy -Rozkładanie wielomianu na czynniki
Wyjęcie wspólnego czynnika z nawiasów
Metoda grupowania
Skrócona formuła mnożenia
Podsumowanie lekcji. Uczniowie odpowiadają na pytania:Jakie zadanie postawiliśmy? Czy udało nam się rozwiązać nasz problem? Jak? Jakie były wyniki? Jak rozłożyć wielomian na czynniki? Do jakich zadań można wykorzystać tę wiedzę? Co robiłeś dobrze w klasie? Nad czym jeszcze trzeba popracować?
Podczas lekcji uczniowie oceniali siebie, na koniec lekcji proszeni są o zsumowanie punktów i wystawienie oceny zgodnie z proponowaną skalą.
Ostatnie słowo nauczyciela: Dzisiaj na lekcji nauczyliśmy się określać, jakie metody należy zastosować, aby rozłożyć wielomiany na czynniki. Aby skonsolidować wykonaną pracę
Praca domowa: §19, #708, #710
Zadanie dodatkowe:
Rozwiąż równanie x 3 + 4x 2 = 9x + 36
Pojęcia „wielomian” i „faktoryzacja wielomianu” w algebrze są bardzo powszechne, ponieważ trzeba je znać, aby łatwo wykonywać obliczenia z dużymi liczbami wielowartościowymi. W tym artykule opiszemy kilka metod dekompozycji. Wszystkie są dość proste w użyciu, wystarczy wybrać odpowiedni w każdym przypadku.
Wielomian to suma jednomianów, czyli wyrażeń zawierających tylko operację mnożenia.
Na przykład 2 * x * y jest jednomianem, ale 2 * x * y + 25 jest wielomianem, który składa się z 2 jednomianów: 2 * x * y i 25. Takie wielomiany nazywane są dwumianami.
Czasami, dla wygody rozwiązywania przykładów z wartościami wielowartościowymi, wyrażenie musi zostać przekształcone, na przykład, rozłożone na pewną liczbę czynników, czyli liczby lub wyrażenia, pomiędzy którymi wykonywana jest operacja mnożenia. Istnieje kilka sposobów rozkładania wielomianu na czynniki. Warto rozważyć je zaczynając od tych najbardziej prymitywnych, które stosuje się nawet w klasach podstawowych.

Wzór na rozkładanie wielomianu na czynniki metodą grupowania ogólnie wygląda następująco:
ac + bd + bc + ad = (ac + bc) + (ad + bd)
Jednomiany należy pogrupować tak, aby w każdej grupie pojawił się wspólny czynnik. W pierwszym nawiasie jest to czynnik c, aw drugim - d. Należy to zrobić, aby następnie wyjąć go z nawiasu, upraszczając w ten sposób obliczenia.
Najprostszy przykład rozkładania wielomianu na czynniki przy użyciu metody grupowania podano poniżej:
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b)
W pierwszym nawiasie musisz wziąć terminy ze współczynnikiem a, który będzie wspólny, aw drugim - ze współczynnikiem b. Zwróć uwagę na znaki + i - w gotowym wyrażeniu. Przed jednomianem stawiamy znak, który był w początkowym wyrażeniu. Oznacza to, że musisz pracować nie z wyrażeniem 25a, ale z wyrażeniem -25. Znak minus jest niejako „przyklejony” do wyrażenia za nim i zawsze uwzględnia go w obliczeniach.
W następnym kroku musisz usunąć czynnik, który jest powszechny, z nawiasu. Po to jest grupowanie. Wyjęcie go z nawiasu oznacza wypisanie przed nawiasem (pomijając znak mnożenia) wszystkich tych czynników, które powtarzają się dokładnie we wszystkich terminach znajdujących się w nawiasie. Jeśli w nawiasie nie ma 2, ale 3 lub więcej wyrazów, czynnik wspólny musi być zawarty w każdym z nich, w przeciwnym razie nie można go wyjąć z nawiasu.
W naszym przypadku tylko 2 terminy w nawiasach. Całkowity mnożnik jest natychmiast widoczny. Pierwszy nawias to a, drugi to b. Tutaj musisz zwrócić uwagę na współczynniki cyfrowe. W pierwszym nawiasie oba współczynniki (10 i 25) są wielokrotnościami 5. Oznacza to, że można umieścić w nawiasie nie tylko a, ale także 5a. Przed nawiasem wypisz 5a, a następnie podziel każdy z wyrazów w nawiasach przez wyjęty czynnik wspólny, a także zapisz iloraz w nawiasach, nie zapominając o znakach + i -. Zrób to samo z drugim nawiasem , usuń 7b, ponieważ 14 i 35 wielokrotność 7.
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b) = 5a (2c - 5) + 7b (2c - 5).
Okazało się, że 2 wyrazy: 5a (2c - 5) i 7b (2c - 5). Każdy z nich zawiera czynnik wspólny (całe wyrażenie w nawiasach jest tutaj takie samo, co oznacza, że jest to czynnik wspólny): 2c - 5. Należy go również wyjąć z nawiasu, czyli wyrazy 5a i 7b pozostają w drugim nawiasie:
5a(2c - 5) + 7b(2c - 5) = (2c - 5)*(5a + 7b).
Tak więc pełne wyrażenie to:
10ac + 14bc - 25a - 35b \u003d (10ac - 25a) + (14bc - 35b) \u003d 5a (2c - 5) + 7b (2c - 5) \u003d (2c - 5) * (5a + 7b).
Zatem wielomian 10ac + 14bc - 25a - 35b rozkłada się na 2 czynniki: (2c - 5) i (5a + 7b). Znak mnożenia między nimi można pominąć podczas pisania

Czasami pojawiają się wyrażenia tego typu: 5a 2 + 50a 3, tutaj możesz umieścić w nawiasie nie tylko a lub 5a, ale nawet 5a 2. Zawsze powinieneś starać się wyciągnąć z nawiasu największy możliwy wspólny czynnik. W naszym przypadku, jeśli podzielimy każdy wyraz przez wspólny czynnik, otrzymamy:
5a 2 / 5a 2 = 1; 50a 3 / 5a 2 = 10a(przy obliczaniu ilorazu kilku potęg o równych podstawach, podstawa jest zachowywana, a wykładnik jest odejmowany). Pozostaje więc jeden w nawiasie (w żadnym wypadku nie zapomnij go wpisać, jeśli całkowicie wyjmiesz jeden z terminów z nawiasu) i iloraz dzielenia: 10a. Okazało się, że:
5a 2 + 50a 3 = 5a 2 (1 + 10a)
Dla wygody obliczeń wyprowadzono kilka wzorów. Nazywa się je skróconymi formułami mnożenia i są używane dość często. Te formuły pomagają rozkładać na czynniki wielomiany zawierające potęgi. To kolejny potężny sposób na faktoryzację. Oto one:

Obliczenia na nich są dość proste. Na przykład:
Podobnie do nich wykonuje się operacje według wzoru kwadratu różnicy. Pozostaje różnica w formule kwadratów. Przykłady tej formuły są bardzo łatwe do zidentyfikowania i znalezienia wśród innych wyrażeń. Na przykład:
Ważne jest, aby każdy z terminów był kwadratem jakiegoś wyrażenia. Następnie wielomian ten należy rozłożyć na czynniki przez różnicę równania kwadratów. W tym celu nie jest konieczne, aby druga potęga znajdowała się powyżej liczby. Istnieją wielomiany zawierające duże potęgi, ale nadal odpowiednie dla tych wzorów.
a 8 +10a 4 +25 = (a 4) 2 + 2*a 4 *5 + 5 2 = (a 4 +5) 2
W tym przykładzie 8 może być reprezentowana jako (a 4) 2 , czyli kwadrat pewnego wyrażenia. 25 to 5 2 a 10a to 4 - jest to iloczyn podwójny wyrazów 2*a 4*5. Oznacza to, że wyrażenie to, pomimo obecności stopni z dużymi wykładnikami, można rozłożyć na 2 czynniki, aby później z nimi pracować.
Te same wzory istnieją przy rozkładaniu na czynniki wielomianów zawierających kostki. Są trochę bardziej skomplikowane niż te z kwadratami:
Ostatnie dwie formuły praktycznie nie są używane do rozkładania wielomianu na czynniki, ponieważ są one złożone i dość rzadko można znaleźć wielomiany, które całkowicie odpowiadają takiej strukturze, aby można je było rozłożyć zgodnie z tymi wzorami. Ale nadal musisz je znać, ponieważ będą one wymagane do działań w przeciwnym kierunku - podczas otwierania nawiasów.

Rozważ przykład: 64a 3 − 8b 3 = (4a) 3 − (2b) 3 = (4a − 2b)((4a) 2 + 4a*2b + (2b) 2) = (4a−2b)(16a 2 + 8ab + 4b 2 ).
Wzięliśmy tutaj dość liczby pierwsze, więc od razu widać, że 64a 3 to (4a) 3 , a 8b 3 to (2b) 3 . Zatem ten wielomian jest rozszerzany przez wzór różnicy sześcianów na 2 czynniki. Działania na wzorze sumy kostek są wykonywane przez analogię.
Ważne jest, aby zrozumieć, że nie wszystkie wielomiany można rozłożyć na co najmniej jeden ze sposobów. Ale są takie wyrażenia, które zawierają większe potęgi niż kwadrat lub sześcian, ale można je również rozszerzyć do skróconych form mnożenia. Na przykład: x 12 + 125y 3 =(x 4) 3 +(5y) 3 =(x 4 +5y)*((x 4) 2 − x 4 *5y+(5y) 2)=(x 4 + 5y) ( x 8 – 5x 4 r + 25 lat 2).
Ten przykład zawiera aż 12 stopni. Ale nawet to można rozliczyć za pomocą wzoru sumy sześcianów. Aby to zrobić, musisz przedstawić x 12 jako (x 4) 3, czyli jako sześcian jakiegoś wyrażenia. Teraz zamiast a, musisz go zastąpić w formule. Cóż, wyrażenie 125y 3 to sześcian 5y. Następnym krokiem jest napisanie wzoru i wykonanie obliczeń.

Na początku lub w razie wątpliwości zawsze możesz sprawdzić przez odwrotne mnożenie. Wystarczy otworzyć nawiasy w wynikowym wyrażeniu i wykonać czynności z podobnymi terminami. Metoda ta ma zastosowanie do wszystkich powyższych metod redukcji: zarówno do pracy ze wspólnym czynnikiem i grupowaniem, jak i do operacji na wzorach sześcianów i potęg do kwadratu.
Wielomiany są najważniejszym rodzajem wyrażeń matematycznych. Na podstawie wielomianów skonstruowano układ równań, nierówności i funkcji. Problemy o różnym stopniu złożoności często zawierają etapy wszechstronnej transformacji wielomianów. Ponieważ matematycznie każdy wielomian jest sumą algebraiczną kilku jednomianów, najbardziej fundamentalną i konieczną zmianą jest przekształcenie szeregu wielomianów w iloczyn dwóch (lub więcej) czynników. W równaniach, które mają możliwość zresetowania jednej z części, translacja wielomianu na czynniki pozwala zrównać pewną część z zerem, a tym samym rozwiązać całe równanie.
Poprzednie samouczki wideo pokazały nam, że w algebrze liniowej istnieją trzy główne sposoby tłumaczenia wielomianów na czynniki. Jest to wyjęcie wspólnego czynnika z nawiasów, przegrupowanie według podobnych terminów, przy użyciu skróconych wzorów mnożenia. Jeśli wszystkie elementy wielomianu mają jakąś wspólną podstawę, to można ją łatwo wyjąć z nawiasów, pozostawiając resztę podziałów w postaci zmodyfikowanego wielomianu w nawiasach. Najczęściej jednak jeden czynnik nie pasuje do wszystkich jednomianów, wpływając tylko na część z nich. W tym przypadku druga część jednomianów może mieć swoją wspólną podstawę. W takich przypadkach stosuje się metodę grupowania – w rzeczywistości uwzględnienie kilku czynników w nawias i utworzenie złożonego wyrażenia, które można przekształcić w inny sposób. I wreszcie cały kompleks specjalnych formuł. Wszystkie są tworzone przez abstrakcyjne obliczenia metodą najprostszego mnożenia wyraz po wyrazie. Podczas obliczeń wiele elementów w wyrażeniu początkowym jest redukowanych, pozostawiając małe wielomiany. Aby nie przeprowadzać za każdym razem pojemnych obliczeń, można skorzystać z gotowych formuł, ich odwrotnych wariantów lub uogólnionych wniosków z tych formuł.

W praktyce często zdarza się, że w jednym ćwiczeniu trzeba połączyć kilka technik, w tym te z kategorii przekształceń wielomianowych. Rozważ przykład. Rozkład na czynniki dwumianowe:
Wyciągamy wspólny czynnik 3 z nawiasów:
3x3 - 3x2 = 3x(x2 - y2)
Jak widać na filmie, drugie nawiasy zawierają różnicę kwadratów. Stosujemy odwrotny skrócony wzór mnożenia, otrzymując:
3x(x2 - y2) = 3x(x + y)(x - y)
Inny przykład. Przekształćmy wyrażenie postaci:
18a2 - 48a + 32
Zmniejszamy współczynniki liczbowe, umieszczając w nawiasach dwójkę:
18a2 - 48a + 32 = 2(9a2 - 24a + 16)

Aby znaleźć odpowiedni skrócony wzór mnożenia dla tego przypadku, należy nieco dostosować wyrażenie, dopasowując wzór do warunków:
2(9a2 - 24a + 16) = 2((3a)2 - 2(3a)4 + (4)2)
Czasami formuła w mylącym wyrażeniu nie jest łatwa do zauważenia. Należy zastosować metody rozkładania wyrażenia na elementy składowe lub dodać wyimaginowane pary konstrukcji, takie jak +x-x. Korygując wyrażenie, musimy przestrzegać zasad sukcesji znaków i zachowania znaczenia wyrażenia. Jednocześnie należy starać się doprowadzić wielomian do pełnej zgodności z abstrakcyjną wersją wzoru. W naszym przykładzie stosujemy wzór kwadratu różnicy:
2((3a)2 - 2(3a)4 + (4)2) = 2(3a - 4)
Zróbmy trudniejsze ćwiczenie. Rozłóżmy wielomian na czynniki:
U3 - 3lata + 6lat - 8
Na początek przeprowadźmy wygodne grupowanie - pierwszy i czwarty element w jedną grupę, drugi i trzeci - w drugą:
Y3 - 3y2 + 6y - 8 = (y3 - 8) - (3y2 - 6y)
Zauważ, że znaki w drugim nawiasie zostały odwrócone, ponieważ przenieśliśmy minus z wyrażenia. W pierwszych nawiasach możemy napisać:
(y3 - (2)3) - (3y2 - 6 lat)
Pozwala to zastosować zmniejszoną formułę mnożenia, aby znaleźć różnicę sześcianów:
(y3 - (2)3) - (3y2 - 6y) = (y - 2) (y2 + 2y + 4) - (3y2 - 6y)

Z drugiego nawiasu wyjmujemy dzielnik wspólny 3y, po czym z całego wyrażenia (dwumianowego) wyjmujemy nawiasy (y - 2), podajemy podobne wyrazy:
(y - 2)(y2 + 2y + 4) - (3y2 - 6y) = (y - 2)(y2 + 2y + 4) - 3y(y - 2) =
\u003d (y - 2) (y2 + 2y + 4 - 3y) \u003d (y - 2) (y2 - y + 4)
W ogólnym przybliżeniu istnieje pewien algorytm działań przy rozwiązywaniu takich ćwiczeń.
1. Poszukujemy wspólnych czynników dla całego wyrażenia;
2. Grupujemy podobne jednomiany, szukamy dla nich wspólnych czynników;
3. Staramy się ująć w nawias najbardziej odpowiednie wyrażenie;
4. Stosujemy wzory skróconego mnożenia;
5. Jeśli na pewnym etapie proces nie przebiega, wprowadzamy wyimaginowaną parę wyrażeń postaci -x + x lub inne konstrukcje samoznoszące się;
6. Podajemy podobne terminy, redukujemy zbędne elementy
Wszystkie punkty algorytmu rzadko znajdują zastosowanie w jednym zadaniu, ale ogólny przebieg rozwiązywania dowolnego ćwiczenia na dany temat można prześledzić w określonej kolejności.
istnieje kilka różnych sposobów faktoryzacja wielomianu. Najczęściej w praktyce stosuje się nie jedną, ale kilka metod jednocześnie. Tutaj nie może być określonej kolejności działań, w każdym przykładzie wszystko jest indywidualne. Ale możesz spróbować wykonać następującą kolejność:
1. Jeśli istnieje wspólny czynnik, wyjmij go z nawiasu;
2. Następnie spróbuj rozłożyć wielomian na czynniki, używając skróconych wzorów mnożenia;
3. Jeśli po tym nie otrzymaliśmy jeszcze pożądanego rezultatu, powinniśmy spróbować użyć metody grupowania.
1. a^2 - b^2 = (a+b)*(a-b);
2. (a+b)^2 = a^2+2*a*b+b^2;
3. (a-b)^2 = a^2-2*a*b+b^2;
4. a^3+b^3 = (a+b)*(a^2 - a*b+b^2);
5. a^3 - b^3 = (a-b)*(a^2 + a*b+b^2);
Przyjrzyjmy się teraz kilku przykładom:
Przykład 1
Rozkład wielomianu na czynniki: (a^2+1)^2 - 4*a^2
Najpierw stosujemy skróconą formułę mnożenia „różnica kwadratów” i otwieramy nawiasy wewnętrzne.
(a^2+1)^2 - 4*a^2 = ((a^2+1)-2*a)*((a^2+1)+2*a) = (a^2+1 -2*a)*(a^2+1+2*a);
Zauważ, że wyrażenia dla kwadratu sumy i kwadratu różnicy dwóch wyrażeń są otrzymywane w nawiasach. Zastosuj je i uzyskaj odpowiedź.
a^2+1-2*a)*(a^2+1+2*a) = (a-1)^2*(a+1)^2;
Odpowiadać:(a-1)^2*(a+1)^2;
Przykład 2
Faktoryzacji wielomianu 4*x^2 - y^2 + 4*x +2*y.
Jak widać bezpośrednio tutaj, żadna z metod nie jest odpowiednia. Ale są dwa kwadraty, można je pogrupować. Spróbujmy.
4*x^2 - y^2 + 4*x +2*y = (4*x^2 - y^2) +(4*x +2*y);
Otrzymaliśmy wzór na różnicę kwadratów w pierwszym nawiasie, a w drugim nawiasie jest wspólny czynnik dwójki. Zastosujmy wzór i usuńmy wspólny czynnik.
(4*x^2 - y^2) +(4*x +2*y)= (2*x - y)*(2*x+y) +2*(2*x+y);
Widać, że otrzymuje się dwa identyczne nawiasy. Wyjmujemy je jako wspólny czynnik.
(2*x - y)*(2*x+y) +2*(2*x+y) = (2*x+y)*(2*x - y)+2)= (2*x+ y )*(2*x-y+2);
Odpowiadać:(2*x+y)*(2*x-y+2);
Jak widać, nie ma uniwersalnej drogi. Wraz z doświadczeniem nadejdzie umiejętność i rozłożenie wielomianu na czynniki będzie bardzo łatwe.