Раздели: Математика
Тип урок:
Цел:формират способността да факторизират полином.
Задачи:
Методи на работа:
Оборудване на урока:интерактивна бяла дъска или скоп, таблици със съкратени формули за умножение, инструкции, листовка за групова работа.
Структура на урока:
По време на часовете
1. Организационен момент
Учителят проверява готовността на класната стая и учениците за урока.
2. Формулиране на темата, целите и задачите на урока-практика
3. Проверка на домашните
На дъската има примери за решаване на домашни упражнения No 943 (a, c); № 945 (c, d). Пробите са направени от учениците от класа. (Тази група ученици беше идентифицирана в предишния урок, те формализираха решението си в междучасието). Учениците се подготвят да „защитят” решенията.
Учител:
Проверява домашните в ученическите тетрадки.
Кани учениците от класа да отговорят на въпроса: „Какви трудности предизвика заданието?“.
Предлага да сравни своето решение с решението на дъската.
Кани учениците на дъската да отговорят на въпросите, които учениците имаха на терен при проверка на образците.
Коментира отговорите на учениците, допълва отговорите, обяснява (ако е необходимо).
Обобщава домашното.
Ученици:
Представете домашното на учителя.
Сменяйте тетрадките (по двойки) и проверявайте помежду си.
Отговорете на въпросите на учителя.
Проверете решението си с мостри.
Те действат като опоненти, правят допълнения, корекции, записват различен метод, ако методът за решаване в тетрадката се различава от метода на дъската.
Поискайте необходимите обяснения на учениците, на учителя.
Намерете начини да проверите резултатите.
Участвайте в оценката на качеството на задачите на дъската.
4. Актуализиране на основните знания и умения на учениците
1. Устна работа
Учител:
Отговори на въпросите:
2. Полиномите са написани на дъската:
1. 14x 3 - 14x 5
2. 16x 2 - (2 + x) 2
3. 9 - x 2 - 2xy - y 2
4.x3 - 3x - 2
Учителкани учениците да факторизират полиноми № 1-3:
На един ученик се предлага да разложи на множители полином № 4 (индивидуална задача с повишена трудност, задачата се изпълнява на формат А 4). След това на дъската се появява примерно решение на задачи No 1-3 (изпълнено от учителя), примерно решение на задача No 4 (изпълнено от ученика).
3. Загрейте
Учителят дава инструкции за разлагане и избор на буквата, свързана с верния отговор. Като добавите буквите, ще получите името на най-великия математик от 17 век, който има огромен принос в развитието на теорията за решаване на уравнения. (Декарт)
5. Физическо възпитание Учениците четат твърденията. Ако твърдението е вярно, тогава учениците трябва да вдигнат ръце, а ако не е вярно, тогава да седнат на бюрото. (приложение 2)
6. Инструкция за изпълнение на задачите от семинара.
На интерактивна дъска или отделен плакат, таблица с инструкции.
При разлагане на полином на множители трябва да се спазва следният ред:
1. поставете общия множител извън скоби (ако има такъв);
2. приложете формули за съкратено умножение (ако е възможно);
3. прилага метода на групиране;
4. проверка на резултата, получен чрез умножение.
Учител:
Предлага инструкции на учениците (подчертава стъпка 4).
Предлага изпълнение на работни задачи по групи.
Разпределя работни листове по групи, листове с копирна хартия за попълване на задачи в тетрадки и последващата им проверка.
Определя времето за работа по групи, за работа в тетрадки.
студенти:
Те четат инструкциите.
Учителите слушат внимателно.
Те са настанени на групи (по 4-5 души).
Подгответе се за практическа работа.
7. Изпълнение на задачи по групи
Работни листове със задачи за групи. (приложение 3)
Учител:
Ръководи самостоятелна работа в групи.
Оценява се способността на учениците за самостоятелна работа, умението за работа в група, качеството на оформянето на работния лист.
студенти:
Изпълнете задачи върху листове карбон, приложени в работна тетрадка.
Обсъдете рационални решения.
Подгответе работен лист за групата.
Подгответе се да защитите работата си.
8. Проверка и обсъждане на заданието
Отговори на бялата дъска.
Учител:
Събира преписи от решения.
Ръководи работата на учениците, отчитайки работните листове.
Предлага да извърши самооценка на работата си, да сравни отговорите в тетрадки, работни листове и образци на дъската.
Припомня критериите за оценяване на работата, за участие в нейното изпълнение.
Осигурява разяснения относно възникващи въпроси, свързани с решения или самооценка.
Обобщава първите резултати от практическата работа и размисъл.
Обобщава (съвместно с учениците) урока.
Казва, че окончателните резултати ще бъдат обобщени след проверка на копия от работата, извършена от учениците.
студенти:
Дайте копия на учителя.
Работните листове са прикрепени към дъската.
Отчитане на изпълнението на работата.
Извършване на самооценка и самооценка на изпълнението на работата.
9. Поставяне на домашна работа
Домашната работа е написана на дъската: No 1016 (a, b); 1017 (c, d); № 1021 (d, e, f)*
Учител:
Предлага да напише задължителната част от задачата у дома.
Дава коментар за изпълнението му.
Кани по-подготвените ученици да запишат № 1021 (d, e, f) *.
Казва ви да се подготвите за следващия урок за преглед
ПЛАН НА УРОКА
Тип урок : урок обучение на нов материал, базирано на проблемно обучение9 Цел на урока
създават условия за упражняване на уменията и способностите за разлагане на многочлен с различни методи.
10. Задачи:
Образователни
повторете алгоритмите на операциите: изваждане на общия множител от скобата, метод на групиране, формули за съкратено умножение.
изграждане на умения:
– прилагат знания по темата „факторизация на многочлен по различни начини“;
– изпълняват задачи според избрания метод на действие;
– изберете най-рационалния начин за рационализиране на изчисленията, трансформирайте полиноми.
Образователни
да насърчава развитието на когнитивните способности, вниманието, паметта, мисленето на учениците чрез използване на различни упражнения;
развиват умения самостоятелна работаи групова работа; поддържат интереса на учениците към математиката
възпитатели
поддържат интереса на учениците към математиката
11. Оформен UUD
лични: осъзнаване на целта на дейността (очакван резултат), осъзнаване или избор на метод на дейност (Как ще го направя? Как ще получа резултата?), анализ и оценка на резултата; оценка на техните възможности;
Регулаторни: вземат предвид правилото при планиране и контролиране на начина на решаване, планиране, оценка на резултатите от работата;
Когнитивни: избор на най ефективни начинирешаване на проблеми, структуриране на знания;преобразуване на информация от една форма в друга.
Комуникативен: планиранеобразователно сътрудничество с учителя и връстниците, спазване на правилата за речево поведение, способност за изразяване иобосновават своята гледна точка, вземат предвид различните мнения и се стремят да координират различни позиции в сътрудничество.
12. Методи:
по източници на знания: вербални, визуални;
по отношение на характера на познавателната дейност: репродуктивна, частично изследователска.
13. Форми на работа на студентите: фронтален, индивидуален, групов.
14. Необходимо Техническо оборудване: компютър, проектор, интерактивна дъска, раздавателни материали (лист за самоконтрол, карти със задачи), електронна презентация, изработена по програматамощностточка
15.Планирани резултати :
Лична възпитаване на чувство за самоуважение и взаимно уважение; развитие на сътрудничеството при работа в групи;
Метасубект развитие на речта; развитие на самостоятелността на учениците; развитие на внимание при търсене на грешки.
предмет развитие на умения за работа с информация, овладяване на решения
По време на часовете:
1. Поздрав към учениците. Проверка на готовността на класа за урока от учителя; организация на вниманието; урок за лист за оценкаПриложение 1 , прецизиране на критериите за оценка.
Проверка на домашните и актуализиране на знанията
1. 3а + 6b= 3(a + 2b)2. 100 - 20s + s 2 = (10 + s) 2
3. с 2 - 81 \u003d (s - 9) (s + 9)
4. 6x 3 – 5 пъти 4 = х 4 (6x - 5)
5. ay - 3y - 4a + 12 \u003d y (a - 3) - 4 (a - 3)
6. 0,09x 2 - 0,25 г 2 \u003d (0,03x - 0,05y) (0,03x + 0,05y)
7. c (x - 3) -д(x - 3) \u003d (x - 3) (s -д)
8. 14x 2 - 7x \u003d 7x (7x - 1)
9. -1600 + а 12 = (40 + a 6 ) (40 - а 6 )
10,9x 2 – 24xy + 16y 2 = (3x - 4y) 2
11.8s 3 – 2s 2 + 4s - 1 =
2s 2 (4s - 1) + (4s - 1) = (4s - 1)2s 2
12. b 4 + с 2 – 2 b 2 c = (b – ° С) 2
(задачи за домашна работа, взети от учебника, включват разлагане на множители по различни начини. За да завършите тази работаУчениците трябва да си припомнят какво са научили досега
Отговорите, записани на слайда, съдържат грешки, учениците се научават да виждат начини и също така, забелязвайки грешки, запомнят начини за действие,
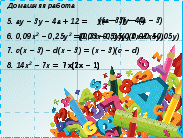

Учениците по групи след проверка на домашната работа дават точки за свършената работа.
2 РелеПриложение 2 (членовете на екипа се редуват да изпълняват задачата, докато стрелката свързва примера и начина, по който е разложен)
3а-12б = 3(а – 4 б)2а + 2б + а 2 +аб = (а + б) (2 + а)
9а 2 – 16б 2 = ( 3а - 4 b)(3a + 4b)
16а 2 - 8ab+b 2 = (4а – б) 2
7а 2 b-14ab 2 + 7ab = 7ab(a - 2b + 1)
а 2 + ab- a - ac- bc + c = (a + b - 1) (a - c)
25а 2 + 70ab + 49b 2 = ( 5а + 7 б) 2
5x 2 - 45 г 2 \u003d 5 (x - 3y) (x + 3y)
![]()
Не се факторизира
Метод на групиране

С помощта на слайда се проверява свършената работа и се обръща внимание на факта, че последният пример трябва да се комбинира с два метода на разлагане (заграждане на общия множител и формулата за съкратено умножение)
Учениците оценяват свършената работа, вписват резултатите в листовете за оценка, а също така формулират темата на урока.

3. Изпълнение на задачи (учениците са поканени да изпълнят задачата. Обсъждайки решението в група, момчетата стигат до извода, че са необходими няколко начина за факторизиране на тези полиноми. Екипът, който първи предложи правилното разлагане, има право да запише решението си на дъската, останалите го записват в тетрадка .. Екипът е установил работа в помощ на ученици, които се затрудняват да се справят със задачата)
1) 2а 2 - 2б 25) 5м 2 + 5n 2 – 10 мин
9) 84 - 42y - 7xy + 14x
13) х 2 y+14xy 2 + 49 г 3
2) 3а 2 + 6ab + 3b 2
6) cx 2 – cy 2
10) -7б 2 – 14 пр.н.е. – 7в 2
14) 3ab 2 – 27а
3) х 3 – 4 пъти
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8а 3 б+56а 2 b 2 – 98аб 3
4) 3ab + 15b - 3a - 15
8) х 4 - х 2
12) ° С 4 - 81
16) 0 , 09т 4 - T 6
4. Крайният етап –Факторизиране на полином
Изваждане на общия множител извън скоби
Метод на групиране
Формула за съкратено умножение
Обобщение на урока. Учениците отговарят на въпросите:Каква задача си поставихме? Успяхме ли да решим проблема си? как? Какви бяха резултатите? Как може да се разложи полином? За какви задачи могат да се приложат тези знания? Какво направи добре в клас? Върху какво още трябва да се работи?
По време на урока учениците се самооцениха, в края на урока те бяха помолени да съберат оценките и да дадат оценка в съответствие с предложената скала.
Заключителна дума на учителя: Днес в урока се научихме да определяме какви методи трябва да се прилагат, за да се факторизират полиноми. За консолидиране на свършената работа
Домашна работа: §19, #708, #710
Допълнителна задача:
Решете уравнението x 3 + 4x 2 = 9x + 36
Понятията "полином" и "факторизация на полином" в алгебрата са много често срещани, защото трябва да ги знаете, за да извършвате лесно изчисления с големи многозначни числа. Тази статия ще опише няколко метода на разлагане. Всички те са доста лесни за използване, просто трябва да изберете правилния във всеки случай.
Полиномът е сборът от мономи, т.е. изрази, съдържащи само операцията умножение.
Например 2 * x * y е моном, но 2 * x * y + 25 е полином, който се състои от 2 монома: 2 * x * y и 25. Такива полиноми се наричат биноми.
Понякога, за удобство на решаването на примери с многозначни стойности, изразът трябва да бъде трансформиран, например, разложен на определен брой фактори, тоест числа или изрази, между които се извършва операцията за умножение. Има редица начини за факторизиране на полином. Струва си да ги разгледаме, като започнем от най-примитивния, който се използва дори в началните класове.

Формулата за разлагане на полином на фактори чрез метода на групиране като цяло изглежда така:
ac + bd + bc + ad = (ac + bc) + (ad + bd)
Необходимо е мономите да се групират така, че във всяка група да се появи общ фактор. В първата скоба това е факторът c, а във втората - d. Това трябва да се направи, за да го извадите от скобата, като по този начин опростите изчисленията.
Най-простият пример за разлагане на полином на фактори с помощта на метода на групиране е даден по-долу:
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b)
В първата скоба трябва да вземете термините с коефициента a, които ще бъдат общи, а във втората - с коефициента b. Обърнете внимание на знаците + и - в готовия израз. Поставяме пред монома знака, който беше в първоначалния израз. Тоест, трябва да работите не с израза 25a, а с израза -25. Знакът минус, така да се каже, е „залепен“ към израза зад него и винаги го взема предвид при изчисленията.
На следващата стъпка трябва да извадите фактора, който е често срещан, извън скобата. За това е групирането. Да го извадим от скобата означава да изпишем преди скобата (без знака за умножение) всички онези множители, които се повтарят точно във всички членове, които са в скобата. Ако в скобата има не 2, а 3 или повече члена, общият множител трябва да се съдържа във всеки от тях, в противен случай той не може да бъде изваден от скобата.
В нашия случай само 2 термина в скоби. Общият множител се вижда веднага. Първата скоба е a, втората е b. Тук трябва да обърнете внимание на цифровите коефициенти. В първата скоба и двата коефициента (10 и 25) са кратни на 5. Това означава, че не само a, но и 5a могат да бъдат поставени в скоби. Преди скобата напишете 5a и след това разделете всеки от членовете в скоби на извадения общ множител и също запишете частното в скоби, без да забравяте знаците + и -. Направете същото с втората скоба , извадете 7b, тъй като 14 и 35 са кратни на 7.
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b) = 5a (2c - 5) + 7b (2c - 5).
Оказаха се 2 члена: 5a (2c - 5) и 7b (2c - 5). Всеки от тях съдържа общ множител (целият израз в скоби тук е един и същ, което означава, че е общ множител): 2c - 5. Той също трябва да бъде изваден от скобите, тоест членовете 5a и 7b остават във втората скоба:
5a(2c - 5) + 7b(2c - 5) = (2c - 5)*(5a + 7b).
Така че пълният израз е:
10ac + 14bc - 25a - 35b \u003d (10ac - 25a) + (14bc - 35b) \u003d 5a (2c - 5) + 7b (2c - 5) \u003d (2c - 5) * (5a + 7b).
Така полиномът 10ac + 14bc - 25a - 35b се разлага на 2 фактора: (2c - 5) и (5a + 7b). Знакът за умножение между тях може да се пропуска при писане

Понякога има изрази от този тип: 5a 2 + 50a 3, тук можете да поставите в скоби не само a или 5a, но дори 5a 2. Винаги трябва да се опитвате да извадите възможно най-големия общ множител от скобата. В нашия случай, ако разделим всеки член на общ множител, получаваме:
5a 2 / 5a 2 = 1; 50a 3 / 5a 2 = 10a(при изчисляване на частното на няколко степени с еднакви основи, основата се запазва, а показателят се изважда). Така в скобата остава единица (в никакъв случай не забравяйте да я напишете, ако извадите изцяло един от членовете от скобата) и частното при деление: 10a. Оказва се, че:
5a 2 + 50a 3 = 5a 2 (1 + 10a)
За удобство на изчисленията са изведени няколко формули. Наричат се формули за намалено умножение и се използват доста често. Тези формули помагат за факторизиране на полиноми, съдържащи степени. Това е още един ефективен начинфакторизации. И така, ето ги:

Изчисленията върху тях се правят съвсем просто. Например:
Операциите по формулата на квадрата на разликата се извършват подобно на тези. Това, което остава, е формулата за разликата на квадратите. Примерите за тази формула са много лесни за идентифициране и намиране сред други изрази. Например:
Важно е всеки от членовете да е квадрат на някакъв израз. Тогава този полином трябва да бъде разложен на множители по формулата за разликата на квадратите. За това не е необходимо втората степен да е над числото. Има полиноми с големи степени, но все пак подходящи за тези формули.
a 8 +10a 4 +25 = (a 4) 2 + 2*a 4 *5 + 5 2 = (a 4 +5) 2
AT този примери 8 може да бъде представено като (a 4) 2, тоест квадрат на определен израз. 25 е 5 2 и 10a е 4 - това е двойното произведение на членовете 2*a 4 *5. Тоест, този израз, въпреки наличието на степени с големи показатели, може да се разложи на 2 фактора, за да се работи с тях по-късно.
Съществуват същите формули за разлагане на полиноми, съдържащи кубове. Те са малко по-сложни от тези с квадратите:
Последните две формули практически не се използват за целите на факторизирането на полином, тъй като са сложни и е доста рядко да се намерят полиноми, които напълно отговарят на точно такава структура, така че да могат да бъдат разложени по тези формули. Но все пак трябва да ги знаете, тъй като те ще са необходими за действия в обратна посока - при отваряне на скоби.

Помислете за пример: 64a 3 − 8b 3 = (4a) 3 − (2b) 3 = (4a − 2b)((4a) 2 + 4a*2b + (2b) 2) = (4a−2b)(16a 2 + 8ab + 4b 2 ).
Тук сме взели доста прости числа, така че можете веднага да видите, че 64a 3 е (4a) 3 и 8b 3 е (2b) 3 . По този начин този полином се разширява чрез формулата за разлика на кубове на 2 фактора. Действията върху формулата на сумата от кубчета се извършват по аналогия.
Важно е да се разбере, че не всички полиноми могат да бъдат разложени поне по един от начините. Но има такива изрази, които съдържат по-големи степени от квадрат или куб, но те също могат да бъдат разширени в съкратени форми за умножение. Например: x 12 + 125y 3 =(x 4) 3 +(5y) 3 =(x 4 +5y)*((x 4) 2 − x 4 *5y+(5y) 2)=(x 4 + 5y) ( x 8 − 5x 4 y + 25y 2).
Този пример съдържа цели 12 градуса. Но дори и той може да бъде разложен на множители с помощта на формулата за сбора на кубовете. За да направите това, трябва да представите x 12 като (x 4) 3, тоест като куб на някакъв израз. Сега, вместо a, трябва да го замените във формулата. Е, изразът 125y 3 е кубът на 5y. Следващата стъпка е да напишете формулата и да направите изчисленията.

В началото или когато се съмнявате, винаги можете да проверите чрез обратно умножение. Трябва само да отворите скобите в получения израз и да извършите действия с подобни термини. Този метод се прилага за всички горепосочени методи за намаляване: както за работа с общ фактор и групиране, така и за операции върху формулите на кубове и квадратни степени.
Полиномите са най-важният тип математически изрази. На базата на полиноми е построен набор от уравнения, неравенства и функции. Проблемите с различни нива на сложност често съдържат етапи на разнообразна трансформация на полиноми. Тъй като математически всеки полином е алгебрична сума от няколко мономи, най-фундаменталната и необходима промяна е трансформирането на полиномна серия в продукт на два (или повече) фактора. В уравнения, които имат способността да нулират една от частите, преобразуването на полинома в множители ви позволява да приравните част към нула и по този начин да решите цялото уравнение.
Предишните видео уроци ни показаха, че в линейната алгебра има три основни начина за преобразуване на полиноми в фактори. Това е изваждане на общия множител извън скоби, прегрупиране според подобни термини, като се използват формули за съкратено умножение. Ако всички членове на полинома имат някаква обща основа, тогава тя може лесно да бъде извадена от скобите, оставяйки остатъка от деленията под формата на модифициран полином в скоби. Но най-често един фактор не отговаря на всички мономи, засягайки само част от тях. В този случай другата част от мономите може да има собствена обща основа. В такива случаи се използва метод на групиране - всъщност поставяне в скоби на няколко фактора и създаване на сложен израз, който може да бъде трансформиран по други начини. И накрая, има цял комплекс от специални формули. Всички те се формират чрез абстрактни изчисления, като се използва методът на най-простото умножение член по член. По време на изчисленията много елементи в първоначалния израз се редуцират, оставяйки малки полиноми. За да не извършвате обемни изчисления всеки път, можете да използвате готови формули, техните обратни варианти или обобщени заключения на тези формули.

На практика често се случва в едно упражнение да се комбинират няколко техники, включително и от категорията на полиномните трансформации. Помислете за пример. Разложете на множители по бином:
Изваждаме общия множител 3 извън скоби:
3x3 - 3x2 = 3x(x2 - y2)
Както можете да видите във видеото, вторите скоби съдържат разликата на квадратите. Прилагаме обратната формула за съкратено умножение, получавайки:
3x(x2 - y2) = 3x(x + y)(x - y)
Друг пример. Нека трансформираме израз от формата:
18а2 - 48а + 32
Намаляваме числовите коефициенти, като поставяме двойката в скоби:
18a2 - 48a + 32 = 2(9a2 - 24a + 16)

За да се намери подходяща съкратена формула за умножение за този случай, е необходимо леко да коригирате израза, като приспособите формулата към условията:
2(9a2 - 24a + 16) = 2((3a)2 - 2(3a)4 + (4)2)
Понякога формула в объркващ израз не се вижда толкова лесно. Човек трябва да приложи методите за разлагане на израза на съставните му елементи или да добави въображаеми двойки конструкции, като +x-x. Коригирайки израза, трябва да спазваме правилата за последователност на знаците и запазването на смисъла на израза. В същото време трябва да се опитате да приведете полинома в пълно съответствие с абстрактната версия на формулата. В нашия пример прилагаме формулата на квадрата на разликата:
2((3a)2 - 2(3a)4 + (4)2) = 2(3a - 4)
Нека направим по-трудно упражнение. Нека факторизираме полинома:
U3 - 3y2 + 6y - 8
Като начало, нека извършим удобно групиране - първият и четвъртият елемент в една група, вторият и третият - във втората:
Y3 - 3y2 + 6y - 8 = (y3 - 8) - (3y2 - 6y)
Обърнете внимание, че знаците във вторите скоби са обърнати, тъй като преместихме минуса от израза. В първите скоби можем да напишем:
(y3 - (2)3) - (3y2 - 6y)
Това ви позволява да приложите формулата за намалено умножение, за да намерите разликата на кубовете:
(y3 - (2)3) - (3y2 - 6y) = (y - 2) (y2 + 2y + 4) - (3y2 - 6y)

Изваждаме общия фактор 3y от вторите скоби, след което изваждаме скобите (y - 2) от целия израз (бином), даваме подобни условия:
(y - 2)(y2 + 2y + 4) - (3y2 - 6y) = (y - 2)(y2 + 2y + 4) - 3y(y - 2) =
\u003d (y - 2) (y2 + 2y + 4 - 3y) \u003d (y - 2) (y2 - y + 4)
В общо приближение има определен алгоритъм на действия при решаването на такива упражнения.
1. Търсим общи множители за целия израз;
2. Групираме подобни мономи, търсим общи множители за тях;
3. Опитваме се да поставим в скоби най-подходящия израз;
4. Прилагаме формулите на съкратеното умножение;
5. Ако на някакъв етап процесът не върви, въвеждаме въображаема двойка изрази от формата -x + x или други самоотменящи се конструкции;
6. Даваме подобни условия, намаляваме ненужните елементи
Всички точки от алгоритъма рядко са приложими в една задача, но общият ход на решаване на всяко упражнение по тема може да се следва в даден ред.
Съществува няколко различни начинафакторизиране на полином. Най-често на практика се използва не един, а няколко метода наведнъж. Тук не може да има конкретен ред на действията, във всеки пример всичко е индивидуално. Но можете да опитате да следвате следния ред:
1. Ако има общ фактор, тогава го извадете от скобата;
2. След това опитайте да разложите полинома на множители, като използвате формулите за съкратено умножение;
3. Ако след това все още не сме получили желания резултат, трябва да опитаме да използваме метода на групиране.
1. a^2 - b^2 = (a+b)*(a-b);
2. (a+b)^2 = a^2+2*a*b+b^2;
3. (a-b)^2 = a^2-2*a*b+b^2;
4. a^3+b^3 = (a+b)*(a^2 - a*b+b^2);
5. a^3 - b^3 = (a-b)*(a^2 + a*b+b^2);
Сега нека да разгледаме няколко примера:
Пример 1
Факторизирайте полинома: (a^2+1)^2 - 4*a^2
Първо прилагаме формулата за съкратено умножение "разлика на квадратите" и отваряме вътрешните скоби.
(a^2+1)^2 - 4*a^2 = ((a^2+1)-2*a)*((a^2+1)+2*a) = (a^2+1 -2*a)*(a^2+1+2*a);
Обърнете внимание, че изразите за квадрат на сумата и квадрат на разликата на два израза са получени в скоби. Приложете ги и получете отговора.
a^2+1-2*a)*(a^2+1+2*a) = (a-1)^2*(a+1)^2;
Отговор:(a-1)^2*(a+1)^2;
Пример 2
Разложете на множители полинома 4*x^2 - y^2 + 4*x +2*y.
Както можете да видите директно тук, нито един от методите не е подходящ. Но има два квадрата, те могат да бъдат групирани. Да опитаме.
4*x^2 - y^2 + 4*x +2*y = (4*x^2 - y^2) +(4*x +2*y);
Получихме формулата за разликата на квадратите в първата скоба, а във втората скоба има общ множител две. Нека приложим формулата и извадим общия множител.
(4*x^2 - y^2) +(4*x +2*y)= (2*x - y)*(2*x+y) +2*(2*x+y);
Вижда се, че се получават две еднакви скоби. Изваждаме ги като общ фактор.
(2*x - y)*(2*x+y) +2*(2*x+y) = (2*x+y)*(2*x - y)+2)= (2*x+ y) )*(2*x-y+2);
Отговор:(2*x+y)*(2*x-y+2);
Както можете да видите, няма универсален начин. С натрупването на опит, умението ще дойде и разлагането на полинома на множители ще бъде много лесно.