الأقسام: رياضيات
نوع الدرس:
استهداف:تشكيل القدرة على تحليل كثير الحدود إلى عوامل.
مهام:
أساليب العمل:
معدات الدرس:السبورة التفاعلية أو النطاق العلوي ، والجداول مع صيغ الضرب المختصرة ، والتعليمات ، والنشرات للعمل الجماعي.
هيكل الدرس:
خلال الفصول
1. لحظة تنظيمية
يتحقق المعلم من جاهزية الفصل والطلاب للدرس.
2. صياغة موضوع وأهداف وغايات ممارسة الدرس
3. فحص الواجبات المنزلية
على السبورة أمثلة لحل التمارين المنزلية رقم 943 (أ ، ج) ؛ رقم 945 (ج ، د). تم عمل العينات من قبل طلاب الفصل. (تم تحديد هذه المجموعة من الطلاب في الدرس السابق ، وقاموا بإضفاء الطابع الرسمي على قرارهم في العطلة). يستعد الطلاب "للدفاع" عن الحلول.
معلم:
الشيكات للواجب المنزلي في دفاتر ملاحظات الطلاب.
يدعو طلاب الفصل للإجابة على السؤال: "ما الصعوبات التي سببتها المهمة؟".
عروض لمقارنة الحل مع الحل الموجود على السبورة.
دعوة الطلاب على السبورة للإجابة على الأسئلة التي طرحها الطلاب في الميدان عند التحقق من العينات.
يعلق على إجابات الطلاب ، ويكمل الإجابات ، ويشرح (إذا لزم الأمر).
يلخص الواجب المنزلي.
الطلاب:
تقديم الواجب المنزلي للمعلم.
قم بتغيير دفاتر الملاحظات (في أزواج) وتحقق مع بعضها البعض.
أجب علي اسئلة المعلم.
تحقق من الحل الخاص بك مع العينات.
يتصرفون كخصوم ، ويقومون بالإضافات ، والتصحيحات ، ويكتبون طريقة مختلفة إذا كانت طريقة الحل في دفتر الملاحظات تختلف عن الطريقة الموجودة على السبورة.
اطلب التفسيرات اللازمة للطلاب ، للمعلم.
ابحث عن طرق للتحقق من النتائج.
المشاركة في تقييم جودة المهام على السبورة.
4. تحديث المعارف والمهارات الأساسية للطلاب
1. العمل الشفوي
معلم:
أجب على الأسئلة:
2. متعدد الحدود مكتوب على السبورة:
1. 14 × 3 - 14 × 5
2. 16x 2 - (2 + x) 2
3. 9 - × 2 - 2 × ص - ص 2
4.x3 - 3x - 2
معلميدعو الطلاب إلى تحليل كثيرات الحدود رقم 1-3:
يُعرض على أحد الطلاب تحليل كثير الحدود رقم 4 (مهمة فردية ذات صعوبة متزايدة ، يتم تنفيذ المهمة على تنسيق A 4). ثم يظهر نموذج حل للمهام رقم 1-3 (قام به المعلم) ، نموذج حل للمهمة رقم 4 (قام به الطالب) على السبورة.
3. الاحماء
يعطي المعلم تعليمات لتحليل واختيار الحرف المرتبط بالإجابة الصحيحة. من خلال إضافة الأحرف ، ستحصل على اسم أعظم عالم رياضيات في القرن السابع عشر ، والذي قدم مساهمة كبيرة في تطوير نظرية حل المعادلات. (ديكارت)
5. التربية البدنية يقرأ الطلاب البيانات. إذا كانت العبارة صحيحة ، فيجب على الطلاب رفع أيديهم ، وإذا لم يكن ذلك صحيحًا ، فجلسوا على المكتب. (الملحق 2)
6. إرشادات حول كيفية إنجاز مهام الورشة.
على سبورة تفاعلية أو ملصق منفصل ، طاولة بها تعليمات.
عند تحليل كثير الحدود إلى عوامل ، يجب مراعاة الترتيب التالي:
1. ضع العامل المشترك من بين قوسين (إن وجد) ؛
2. تطبيق صيغ الضرب المختصرة (إن أمكن) ؛
3. تطبيق طريقة التجميع.
4. تحقق من النتيجة التي تم الحصول عليها عن طريق الضرب.
معلم:
يقدم تعليمات للطلاب (يؤكد الخطوة 4).
يقدم تنفيذ مهام ورشة العمل في مجموعات.
يوزع أوراق العمل في مجموعات ، أوراق بها ورق كربوني لإكمال المهام في دفاتر الملاحظات والتحقق اللاحق منها.
يحدد وقت العمل في مجموعات ، للعمل في دفاتر الملاحظات.
الطلاب:
قرأوا التعليمات.
يستمع المعلمون بعناية.
يجلسون في مجموعات (4-5 أشخاص لكل منهما).
الاستعداد للعمل العملي.
7. أداء المهام في مجموعات
أوراق العمل مع المهام للمجموعات. (الملحق 3)
معلم:
يدير العمل المستقل في مجموعات.
يقيم قدرة الطلاب على العمل بشكل مستقل ، والقدرة على العمل في مجموعة ، وجودة تصميم ورقة العمل.
الطلاب:
نفذ المهام على أوراق من ورق الكربون مرفقة في مصنف.
ناقش الحلول المنطقية.
قم بإعداد ورقة عمل للمجموعة.
استعد للدفاع عن عملك.
8. فحص ومناقشة المهمة
الإجابات على السبورة.
معلم:
يجمع نسخ من القرارات.
يدير عمل الطلاب على أوراق العمل.
عروض لإجراء تقييم ذاتي لعملهم ، ومقارنة الإجابات في دفاتر الملاحظات وأوراق العمل والعينات على السبورة.
يذكر بمعايير الدرجات للعمل والمشاركة في تنفيذه.
تقديم توضيح بشأن القرارات الناشئة أو قضايا التقييم الذاتي.
يلخص النتائج الأولى للعمل العملي والتفكير.
يلخص (مع الطلاب) الدرس.
يقول أنه سيتم تلخيص النتائج النهائية بعد التحقق من نسخ الأعمال التي قام بها الطلاب.
الطلاب:
أعط نسخا للمعلم.
يتم إرفاق أوراق العمل باللوحة.
الإبلاغ عن أداء العمل.
إجراء التقييم الذاتي والتقييم الذاتي لأداء العمل.
9. تحديد الواجبات المنزلية
الواجب المنزلي مكتوب على السبورة: رقم 1016 (أ ، ب) ؛ 1017 (ج ، د) ؛ رقم 1021 (د ، هـ ، و) *
معلم:
عروض لكتابة الجزء الإلزامي من المهمة في المنزل.
يعطي تعليقا على تنفيذه.
يدعو الطلاب الأكثر استعدادًا لكتابة رقم 1021 (د ، هـ ، و) *.
يخبرك بالاستعداد لدرس المراجعة التالي
خطة الدرس
نوع الدرس : درس تعلم مادة جديدة على أساس التعلم القائم على حل المشكلات9 الغرض من الدرس
خلق الظروف لممارسة مهارات وقدرات تحليل كثير الحدود باستخدام طرق مختلفة.
10. المهام:
تعليمي
كرر خوارزميات العمليات: إخراج العامل المشترك من القوس ، طريقة التجميع ، صيغ الضرب المختصرة.
بناء المهارات:
– تطبيق المعرفة حول موضوع "تحليل كثير الحدود إلى عوامل بطرق مختلفة" ؛
– أداء المهام وفقًا لطريقة العمل المختارة ؛
– اختر الطريقة الأكثر منطقية لترشيد العمليات الحسابية وتحويل كثيرات الحدود.
تعليمي
لتعزيز تنمية القدرات المعرفية والانتباه والذاكرة والتفكير لدى الطلاب من خلال استخدام تمارين مختلفة ؛
تطوير مهارات العمل المستقل والعمل الجماعي ؛ إبقاء الطلاب مهتمين بالرياضيات
المتعلمين
إبقاء الطلاب مهتمين بالرياضيات
11- شكل UUD
شخصي: الوعي بالغرض من النشاط (النتيجة المتوقعة) ، الوعي أو اختيار طريقة النشاط (كيف سأفعل ذلك؟ كيف سأحصل على النتيجة؟) ، تحليل وتقييم النتيجة ؛ تقييم قدراتهم ؛
تنظيمية: تأخذ في الاعتبار القاعدة في التخطيط والتحكم في طريقة حل وتخطيط وتقييم نتائج العمل ؛
ذهني: اختيار أكثر الطرق فعالية لحل المشاكل ، وتنظيم المعرفة ؛تحويل المعلومات من نموذج إلى آخر.
اتصالي: تخطيطالتعاون التربوي مع المعلم وأقرانه ، والالتزام بقواعد السلوك الكلامي ، والقدرة على التعبير وإثبات وجهة نظرهم ، ومراعاة الآراء المختلفة والسعي لتنسيق المواقف المختلفة في التعاون.
12 - الطرق:
حسب مصادر المعرفة: اللفظية ، البصرية ؛
فيما يتعلق بطبيعة النشاط المعرفي: التناسلي ، الاستكشافي جزئيًا.
13. أشكال العمل الطلابي: أمامي ، فردي ، جماعي.
14. ضروري معدات تقنية: الكمبيوتر ، جهاز العرض ، السبورة التفاعلية ، النشرات (ورقة التحكم الذاتي ، بطاقات المهام) ، العرض الإلكتروني الذي تم إجراؤه في البرنامجقوةنقطة
15- النتائج المخطط لها :
شخصي تعزيز الشعور بالاحترام الذاتي والاحترام المتبادل ؛ تنمية التعاون عند العمل في مجموعات ؛
ميتاسوبجيكت تطوير الكلام تنمية استقلالية الطلاب. تنمية الانتباه عند البحث عن الأخطاء.
موضوعات تنمية المهارات للعمل مع المعلومات وإتقان الحلول
خلال الفصول:
1. تحية الطلاب. التحقق من جاهزية الفصل للدرس من قبل المعلم ؛ تنظيم الانتباه؛ ورقة التقييم التعليميالمرفقات 1 ، تنقيح معايير التقييم.
فحص الواجبات المنزلية وتحديث المعرفة
1. 3 أ + 6ب= 3 (أ + 2ب)2. 100 - 20 ثانية + ثانية 2 = (10 + ث) 2
3. مع 2 - 81 \ u003d (ث - 9) (ث + 9)
4. 6x 3 - 5x 4 = س 4 (٦ × - ٥)
5. ay - 3y - 4a + 12 \ u003d y (a - 3) - 4 (a - 3)
6. 0.09x 2 - 0.25 سنة 2 = (0.03 س - 0.05 ص) (0.03 س + 0.05 ص)
7. ج (س - 3) -د(س - 3) \ u003d (س - 3) (ث -د)
8. 14x 2 - 7x = 7x (7x - 1)
9. -1600 + أ 12 = (40 + أ 6 ) (40 - أ 6 )
10.9x 2 - 24xy + 16y 2 = (3x - 4y) 2
11.8 ثانية 3 - 2 ثانية 2 + 4 ث - 1 =
2 ثانية 2 (4 ث - 1) + (4 ث - 1) = (4 ث - 1) 2 ث 2
12. ب 4 + مع 2 – 2 ب 2 ج = (ب – ج) 2
(يتم أخذ الواجبات المنزلية من الكتاب المدرسي ، وتضمين العوامل بطرق مختلفة. لإكمال هذا العمل ، يحتاج الطلاب إلى تذكر المواد التي سبق دراستها)
تحتوي الإجابات المسجلة على الشريحة على أخطاء ، يتعلم الطلاب رؤية الطرق ، وكذلك ملاحظة الأخطاء ، وتذكر طرق التصرف ،
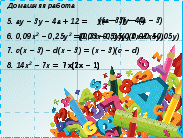

يقوم الطلاب في مجموعات ، بعد التحقق من واجباتهم المنزلية ، بإعطاء نقاط للعمل المنجز.
2 تتابعالملحق 2 (يتناوب أعضاء الفريق على إكمال المهمة ، بينما يربط السهم المثال وطريقة تحللها)
3 أ -12 ب = 3 (أ - 4 ب)2 أ + 2 ب + أ 2 + أب = (أ + ب) (2 + أ)
9 أ 2 - 16 ب 2 = ( 3 أ - 4 ب) (3 أ + 4 ب)
16 أ 2 - 8 أب + ب 2 = (4 أ - ب) 2
7 أ 2 ب 14 أب 2 + 7ab = 7ab (أ - 2 ب + 1)
أ 2 + ab- a - ac- bc + c = (a + b - 1) (a - c)
25 أ 2 + 70ab + 49b 2 = ( 5 أ + 7 ب) 2
5x 2 - 45 سنة 2 = 5 (س - 3 ص) (س + 3 ص)
![]()
لا عامل
طريقة التجميع

بمساعدة الشريحة ، يتم فحص العمل المنجز ، ولفت الانتباه إلى حقيقة أنه يجب دمج المثال الأخير مع طريقتين للتحليل (وضع أقواس بين العامل المشترك وصيغة الضرب المختصرة)
يقوم الطلاب بتقييم العمل المنجز ، وإدخال النتائج في أوراق التقييم ، وكذلك صياغة موضوع الدرس.

3. إكمال المهام (الطلاب مدعوون لإكمال المهمة. بمناقشة الحل في مجموعة ، يتوصل الرجال إلى استنتاج مفاده أن هناك عدة طرق مطلوبة لتحليل هذه كثيرة الحدود إلى عوامل. ويحق للفريق الذي يقدم التحليل الصحيح أولاً أن يكتب حلهم على السبورة ، والبقية يكتبونه في دفتر .. وقد أنشأ الفريق عملًا لمساعدة الطلاب الذين يجدون صعوبة في التعامل مع المهمة)
1) 2 أ 2 - 2 ب 25) 5 م 2 + 5 ن 2 - 10 مليون
9) 84 - 42y - 7xy + 14x
13) x 2 ص + 14 ص 2 + 49 ص 3
2) 3 أ 2 + 6 أب + 3 ب 2
6) cx 2 - سي 2
10) -7 ب 2 - 14 ق.م - 7 ج 2
14) 3 أب 2 - 27 أ
3) x 3 - 4x
7) -3x 2 + 12 س - 12
11) 3x 2 - 3
15) -8 أ 3 ب + 56 أ 2 ب 2 - 98 أب 3
4) 3ab + 15b - 3a - 15
8) x 4 - س 2
12) ج 4 - 81
16) 0 , 09 ت 4 - ت 6
4. المرحلة النهائية -تحليل كثير الحدود
إخراج العامل المشترك من الأقواس
طريقة التجميع
صيغة الضرب المختصرة
ملخص الدرس. يجيب الطلاب على الأسئلة:ما المهمة التي حددناها؟ هل استطعنا حل مشكلتنا؟ كيف؟ ماذا كانت النتائج؟ كيف يمكن تحليل كثير الحدود إلى عوامل؟ لأي مهام يمكن تطبيق هذه المعرفة؟ ماذا فعلت بشكل جيد في الفصل؟ ما الأشياء الأخرى التي يجب العمل عليها؟
أثناء الدرس ، قام الطلاب بتقييم أنفسهم ، وفي نهاية الدرس ، يُطلب منهم جمع الدرجات وإعطاء تقييم وفقًا للمقياس المقترح.
الكلمة الأخيرة للمعلم: تعلمنا اليوم في الدرس تحديد الأساليب التي يجب تطبيقها من أجل تحليل كثيرات الحدود إلى عوامل. لتوحيد العمل المنجز
الواجب المنزلي: §19، # 708، # 710
مهمة إضافية:
حل المعادلة x 3 + 4x 2 = 9 س + 36
تعتبر مفاهيم "كثير الحدود" و "تحليل كثير الحدود إلى عوامل" في الجبر شائعة جدًا ، لأنك تحتاج إلى معرفتها من أجل إجراء العمليات الحسابية بسهولة باستخدام أرقام كبيرة متعددة القيم. ستصف هذه المقالة عدة طرق للتحلل. كل منهم سهل الاستخدام ، ما عليك سوى اختيار الخيار المناسب في كل حالة.
كثير الحدود هو مجموع المونوميرات ، أي التعبيرات التي تحتوي على عملية الضرب فقط.
على سبيل المثال ، 2 * x * y هي أحادية ، لكن 2 * x * y + 25 هي كثيرة الحدود ، والتي تتكون من 2 أحادية: 2 * x * y و 25. تسمى هذه كثيرات الحدود ذات الحدين.
في بعض الأحيان ، لتسهيل حل الأمثلة ذات القيم متعددة القيم ، يجب تحويل التعبير ، على سبيل المثال ، إلى عدد معين من العوامل ، أي الأرقام أو التعبيرات التي يتم تنفيذ عملية الضرب بينها. هناك عدد من الطرق لتحليل كثير الحدود إلى عوامل. يجدر التفكير بها بدءًا من الأكثر بدائية ، والتي تستخدم حتى في الفصول الابتدائية.

تبدو صيغة تحليل كثير الحدود إلى عوامل بطريقة التجميع بشكل عام كما يلي:
ac + bd + bc + ad = (ac + bc) + (ad + bd)
من الضروري تجميع المونوميل بحيث يظهر عامل مشترك في كل مجموعة. في القوس الأول ، هذا هو العامل ج ، وفي الثاني - د. يجب القيام بذلك من أجل إخراجها من القوس ، وبالتالي تبسيط العمليات الحسابية.
فيما يلي أبسط مثال على تحليل كثير الحدود إلى عوامل باستخدام طريقة التجميع:
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b)
في القوس الأول ، يجب أن تأخذ المصطلحات مع العامل أ ، والذي سيكون شائعًا ، وفي الثاني - مع العامل ب. انتبه إلى علامتي + و- في التعبير النهائي. نضع قبل المونومال العلامة التي كانت في التعبير الأولي. أي أنك لا تحتاج إلى العمل مع التعبير 25 أ ، ولكن مع التعبير -25. علامة الطرح ، كما هي ، "مُلصقة" بالتعبير الموجود خلفها وتؤخذها دائمًا في الاعتبار في الحسابات.
في الخطوة التالية ، عليك إخراج العامل المشترك من القوس. هذا ما هو التجمع. لإخراجها من القوس يعني أن تكتب قبل القوس (مع حذف علامة الضرب) كل تلك العوامل التي تتكرر تمامًا في جميع المصطلحات الموجودة بين القوسين. إذا لم يكن هناك 2 ، ولكن 3 مصطلحات أو أكثر في القوس ، فيجب تضمين العامل المشترك في كل منها ، وإلا لا يمكن إزالته من القوس.
في حالتنا ، يوجد حدان فقط بين قوسين. المضاعف الكلي مرئي على الفور. القوس الأول هو أ ، والثاني هو ب. هنا تحتاج إلى الانتباه إلى المعاملات الرقمية. في القوس الأول ، كلا المعاملين (10 و 25) من مضاعفات الرقم 5. وهذا يعني أنه يمكن وضع 5 أ بين قوسين. قبل القوس ، اكتب 5 أ ، ثم اقسم كل مصطلح بين قوسين على العامل المشترك الذي تم حذفه ، واكتب أيضًا حاصل القسمة بين قوسين ، دون أن تنسى علامتي + و-. افعل الشيء نفسه مع القوس الثاني ، أخرج 7 ب ، بما أن 14 و 35 من مضاعفات 7.
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b) = 5a (2c - 5) + 7b (2c - 5).
اتضح فصلين: 5 أ (2 ج - 5) و 7 ب (2 ج - 5). يحتوي كل منها على عامل مشترك (التعبير الكامل بين الأقواس هنا هو نفسه ، مما يعني أنه عامل مشترك): 2 ج - 5. يجب أيضًا إزالته من القوس ، أي المصطلحين 5 أ و 7 ب تبقى في القوس الثاني:
5 أ (2 ج - 5) + 7 ب (2 ج - 5) = (2 ج - 5) * (5 أ + 7 ب).
لذا فإن التعبير الكامل هو:
10ac + 14bc - 25a - 35b \ u003d (10ac - 25a) + (14bc - 35b) \ u003d 5a (2c - 5) + 7b (2c - 5) \ u003d (2c - 5) * (5a + 7b).
وهكذا ، فإن كثير الحدود 10ac + 14bc - 25a - 35b يتحلل إلى عاملين: (2c - 5) و (5a + 7b). يمكن حذف علامة الضرب بينهما عند الكتابة

في بعض الأحيان توجد تعبيرات من هذا النوع: 5a 2 + 50a 3 ، هنا يمكنك وضع قوس ليس فقط على 5a أو 5a ، ولكن حتى 5a 2. يجب أن تحاول دائمًا إخراج أكبر عامل مشترك ممكن من القوس. في حالتنا ، إذا قسمنا كل مصطلح على عامل مشترك ، نحصل على:
5 أ 2/5 أ 2 = 1 ؛ 50 أ 3/5 أ 2 = 10 أ(عند حساب خارج قسمة عدة قوى ذات قواعد متساوية ، يتم الاحتفاظ بالأساس وطرح الأس). وبالتالي ، يبقى المرء بين القوسين (لا تنس بأي حال من الأحوال أن تكتب واحدًا إذا أخرجت أحد المصطلحات من القوس بالكامل) وحاصل القسمة: 10 أ. لقد أتضح أن:
5 أ 2 + 50 أ 3 = 5 أ 2 (1 + 10 أ)
لتسهيل العمليات الحسابية ، تم اشتقاق العديد من الصيغ. يطلق عليهم معادلات الضرب المختزلة ويتم استخدامها في كثير من الأحيان. تساعد هذه الصيغ في تحليل كثيرات الحدود التي تحتوي على قوى. هذه طريقة قوية أخرى للتحليل. إذن ها هم:

يتم إجراء الحسابات عليها بكل بساطة. فمثلا:
يتم تنفيذ العمليات وفقًا لصيغة مربع الفرق بطريقة مماثلة لتلك. ما تبقى هو الفرق في صيغة المربعات. من السهل جدًا تحديد أمثلة هذه الصيغة والعثور عليها من بين التعبيرات الأخرى. فمثلا:
من المهم أن يكون كل مصطلح هو مربع تعبير ما. ثم يتم تحليل كثير الحدود هذا عن طريق صيغة فرق المربعات. لهذا ، ليس من الضروري أن تكون القوة الثانية أعلى من الرقم. هناك كثيرات حدود تحتوي على قوى كبيرة ، لكنها لا تزال مناسبة لهذه الصيغ.
أ 8 + 10 أ 4 +25 = (أ 4) 2 + 2 * أ 4 * 5 + 5 2 = (أ 4 +5) 2
في هذا المثال ، يمكن تمثيل الرقم 8 على أنه (أ 4) 2 ، أي مربع تعبير معين. 25 يساوي 5 2 و 10 أ يساوي 4 - هذا هو المنتج المزدوج للمصطلحات 2 * أ 4 * 5. أي أن هذا التعبير ، على الرغم من وجود الدرجات ذات الأسس الكبيرة ، يمكن أن يتحلل إلى عاملين من أجل العمل معهم لاحقًا.
توجد نفس الصيغ لتحليل كثيرات الحدود التي تحتوي على مكعبات. هم أكثر تعقيدًا قليلاً من أولئك الذين لديهم مربعات:
لا يتم استخدام الصيغتين الأخيرتين عمليًا لغرض تحليل كثير الحدود ، نظرًا لأنها معقدة ، ومن النادر جدًا العثور على كثيرات الحدود التي تتوافق تمامًا مع مثل هذه البنية بحيث يمكن تحللها وفقًا لهذه الصيغ. لكنك لا تزال بحاجة إلى معرفتها ، حيث ستكون مطلوبة لاتخاذ إجراءات في الاتجاه المعاكس - عند فتح الأقواس.

فكر في مثال: 64 أ 3 - 8 ب 3 = (4 أ) 3 - (2 ب) 3 = (4 أ - 2 ب) ((4 أ) 2 + 4 أ * 2 ب + (2 ب) 2) = (4 أ − 2 ب) (16 أ 2 + 8 أب + 4 ب 2 ).
لقد أخذنا هنا أعدادًا أولية إلى حد ما ، لذا يمكنك أن ترى فورًا أن 64a 3 يساوي (4 أ) 3 و 8 ب 3 يساوي (2 ب) 3. وبالتالي ، يتم توسيع هذه كثيرة الحدود باختلاف صيغة المكعبات إلى عاملين. يتم تنفيذ الإجراءات على صيغة مجموع المكعبات عن طريق القياس.
من المهم أن نفهم أنه ليست كل كثيرات الحدود يمكن أن تتحلل بطريقة واحدة على الأقل. لكن توجد مثل هذه التعبيرات التي تحتوي على قوى أكبر من المربع أو المكعب ، ولكن يمكن أيضًا توسيعها إلى أشكال ضرب مختصرة. على سبيل المثال: x 12 + 125y 3 = (x 4) 3 + (5y) 3 = (x 4 + 5y) * ((x 4) 2 - x 4 * 5y + (5y) 2) = (x 4 + 5y) (س 8-5 س 4 ص + 25 ص 2).
يحتوي هذا المثال على ما يصل إلى 12 درجة. لكن حتى يمكن تحليلها إلى عوامل باستخدام صيغة مجموع المكعبات. للقيام بذلك ، عليك تمثيل x 12 كـ (x 4) 3 ، أي كمكعب لبعض التعبيرات. الآن ، بدلاً من a ، تحتاج إلى استبدالها في الصيغة. حسنًا ، المقدار 125y 3 هو مكعب 5y. الخطوة التالية هي كتابة الصيغة وإجراء العمليات الحسابية.

في البداية ، أو عندما تكون في شك ، يمكنك دائمًا التحقق من خلال الضرب العكسي. ما عليك سوى فتح الأقواس في التعبير الناتج وتنفيذ الإجراءات بمصطلحات مماثلة. تنطبق هذه الطريقة على جميع طرق الاختزال المذكورة أعلاه: للعمل مع عامل مشترك وتجميع ، والعمليات على صيغ المكعبات والقوى المربعة.
تعد كثيرات الحدود أهم أنواع التعبيرات الرياضية. على أساس كثيرات الحدود ، تم بناء مجموعة من المعادلات والمتباينات والدوال. غالبًا ما تحتوي المشكلات ذات المستويات المختلفة من التعقيد على مراحل من التحول متعدد الاستخدامات لكثيرات الحدود. نظرًا لأن أي متعدد الحدود من الناحية الرياضية هو مجموع جبري للعديد من المونومرات ، فإن التغيير الأساسي والضروري هو تحويل سلسلة متعددة الحدود إلى منتج من عاملين (أو أكثر). في المعادلات التي لديها القدرة على إعادة تعيين أحد الأجزاء ، تسمح لك ترجمة كثير الحدود إلى عوامل بمساواة جزء ما بالصفر ، وبالتالي حل المعادلة بأكملها.
أظهرت دروس الفيديو السابقة أنه في الجبر الخطي توجد ثلاث طرق رئيسية لترجمة كثيرات الحدود إلى عوامل. يتم إخراج العامل المشترك من الأقواس ، وإعادة التجميع وفقًا لمصطلحات مماثلة ، باستخدام صيغ الضرب المختصرة. إذا كان لجميع أعضاء كثير الحدود أساس مشترك ، فيمكن إزالته بسهولة من الأقواس ، مع ترك باقي الأقسام في شكل متعدد الحدود بين قوسين. ولكن في أغلب الأحيان ، لا يتناسب عامل واحد مع جميع المونوميل ، ويؤثر فقط على جزء منها. في هذه الحالة ، يمكن أن يكون للجزء الآخر من المونومال أساسه المشترك. في مثل هذه الحالات ، يتم استخدام طريقة التجميع - في الواقع ، يتم وضع عدة عوامل بين قوسين وإنشاء تعبير معقد يمكن تحويله بطرق أخرى. وأخيرًا ، هناك مجموعة كاملة من الصيغ الخاصة. يتم تشكيلها جميعًا من خلال حسابات مجردة باستخدام طريقة أبسط عمليات الضرب مصطلحًا بمصطلح. أثناء العمليات الحسابية ، يتم تقليل العديد من العناصر في التعبير الأولي ، تاركًا كثيرات الحدود الصغيرة. من أجل عدم إجراء حسابات واسعة في كل مرة ، يمكنك استخدام الصيغ الجاهزة ، أو نسخها العكسية ، أو الاستنتاجات العامة لهذه الصيغ.

من الناحية العملية ، غالبًا ما يحدث أنه في تمرين واحد ، يجب عليك الجمع بين عدة تقنيات ، بما في ذلك تلك الموجودة في فئة التحويلات متعددة الحدود. تأمل في مثال. عامل بواسطة ذات الحدين:
نأخذ العامل المشترك 3 من الأقواس:
3x3 - 3x2 = 3x (x2 - y2)
كما ترى في الفيديو ، تحتوي الأقواس الثانية على فرق المربعات. نطبق صيغة الضرب المختصرة العكسية ، ونحصل على:
3 س (س 2 - ص 2) = 3 س (س + ص) (س - ص)
مثال آخر. دعنا نحول تعبيرا عن النموذج:
18a2 - 48 أ + 32
نقوم بتقليل المعاملات العددية عن طريق وضع الأقواس بين قوسين:
18a2 - 48a + 32 = 2 (9a2 - 24a + 16)

للعثور على صيغة ضرب مختصرة مناسبة لهذه الحالة ، من الضروري تعديل التعبير قليلاً عن طريق ملاءمة الصيغة للشروط:
2 (9a2 - 24a + 16) = 2 ((3a) 2-2 (3a) 4 + (4) 2)
في بعض الأحيان ، ليس من السهل رؤية صيغة في تعبير محير. يتعين على المرء أن يطبق طرق تحليل التعبير إلى العناصر المكونة له ، أو إضافة أزواج تخيلية من التركيبات ، مثل + x-x. عند تصحيح التعبير ، يجب الالتزام بقواعد تعاقب العلامات ، والحفاظ على معنى التعبير. في الوقت نفسه ، يجب على المرء أن يحاول جعل كثير الحدود يتوافق تمامًا مع النسخة المجردة من الصيغة. في مثالنا ، نطبق صيغة مربع الفرق:
2 ((3 أ) 2-2 (3 أ) 4 + (4) 2) = 2 (3 أ - 4)
لنقم بتمرين أكثر صعوبة. دعنا نتعامل مع كثير الحدود:
U3 - 3y2 + 6y - 8
بادئ ذي بدء ، دعنا ننفذ تجميعًا مناسبًا - العنصر الأول والرابع في مجموعة واحدة ، والثاني والثالث - في المجموعة الثانية:
Y3 - 3y2 + 6y - 8 = (y3 - 8) - (3y2 - 6y)
لاحظ أنه تم عكس الإشارات الموجودة بين الأقواس الثانية ، لأننا نقلنا الناقص من التعبير. يمكننا أن نكتب في الأقواس الأولى:
(y3 - (2) 3) - (3y2 - 6y)
يتيح لك ذلك تطبيق معادلة الضرب المختصرة لإيجاد فرق المكعبات:
(y3 - (2) 3) - (3y2 - 6y) = (y - 2) (y2 + 2y + 4) - (3y2 - 6y)

نخرج العامل المشترك 3y من الأقواس الثانية ، وبعد ذلك نخرج الأقواس (y - 2) من التعبير الكامل (ذي الحدين) ، ونعطي مصطلحات مماثلة:
(ص - 2) (ص 2 + 2 ص + 4) - (3 ص 2 - 6 ص) = (ص - 2) (ص 2 + 2 ص + 4) - 3 ص (ص - 2) =
\ u003d (ص - 2) (y2 + 2y + 4 - 3y) \ u003d (y - 2) (y2 - y + 4)
في التقريب العام ، هناك خوارزمية معينة من الإجراءات عند حل مثل هذه التمارين.
1. نحن نبحث عن العوامل المشتركة للتعبير بأكمله ؛
2. نقوم بتجميع الأحاديات المتشابهة ، والبحث عن العوامل المشتركة لها ؛
3. نحاول وضع التعبير الأنسب بين قوسين ؛
4. نطبق صيغ الضرب المختصر ؛
5. إذا لم تستمر العملية في مرحلة ما ، فإننا ندخل زوجًا تخيليًا من التعبيرات بالصيغة -x + x ، أو إنشاءات أخرى ذاتية الإلغاء ؛
6. نعطي شروط مماثلة ، والحد من العناصر غير الضرورية
نادرًا ما تكون جميع نقاط الخوارزمية قابلة للتطبيق في مهمة واحدة ، ولكن يمكن اتباع المسار العام لحل أي تمرين حول موضوع ما بترتيب معين.
موجود عدة طرق مختلفةتحليل كثير الحدود إلى عوامل. في أغلب الأحيان ، في الممارسة العملية ، لا يتم استخدام طريقة واحدة ، ولكن يتم استخدام عدة طرق في وقت واحد. لا يمكن أن يكون هناك ترتيب محدد للإجراءات هنا ، ففي كل مثال يكون كل شيء فرديًا. ولكن يمكنك محاولة اتباع الترتيب التالي:
1. إذا كان هناك عامل مشترك ، فاخرجه من القوس ؛
2. بعد ذلك ، حاول تحليل كثير الحدود إلى عوامل باستخدام صيغ الضرب المختصرة ؛
3. إذا لم نتلق النتيجة المرجوة بعد ذلك ، يجب أن نحاول استخدام طريقة التجميع.
1. أ ^ 2 - ب ^ 2 = (أ + ب) * (أ-ب) ؛
2. (أ + ب) ^ 2 = أ ^ 2 + 2 * أ * ب + ب ^ 2 ؛
3. (أ-ب) ^ 2 = أ ^ 2-2 * أ * ب + ب ^ 2 ؛
4. أ ^ 3 + ب ^ 3 = (أ + ب) * (أ ^ 2 - أ * ب + ب ^ 2) ؛
5. أ ^ 3 - ب ^ 3 = (أ-ب) * (أ ^ 2 + أ * ب + ب ^ 2) ؛
الآن دعنا نلقي نظرة على بعض الأمثلة:
مثال 1
حلل كثير الحدود إلى عوامل: (a ^ 2 + 1) ^ 2 - 4 * a ^ 2
أولاً ، نطبق صيغة الضرب المختصرة "فرق المربعات" ونفتح الأقواس الداخلية.
(أ ^ 2 + 1) ^ 2 - 4 * أ ^ 2 = ((أ ^ 2 + 1) -2 * أ) * ((أ ^ 2 + 1) + 2 * أ) = (أ ^ 2 + 1 -2 * أ) * (أ ^ 2 + 1 + 2 * أ) ؛
لاحظ أنه تم الحصول على التعبيرات الخاصة بمربع المجموع ومربع الفرق بين تعبيرين بين قوسين. قم بتطبيقها واحصل على الإجابة.
أ ^ 2 + 1-2 * أ) * (أ ^ 2 + 1 + 2 * أ) = (أ -1) ^ 2 * (أ + 1) ^ 2 ؛
إجابه:(أ -1) ^ 2 * (أ + 1) ^ 2 ؛
مثال 2
حلل كثير الحدود إلى عوامل 4 * x ^ 2 - y ^ 2 + 4 * x + 2 * y.
كما ترون هنا مباشرة ، لا توجد طريقة مناسبة. لكن هناك مربعان ، يمكن تجميعهما. لنجرب.
4 * س ^ 2 - ص ^ 2 + 4 * س + 2 * ص = (4 * س ^ 2 - ص ^ 2) + (4 * س + 2 * ص) ؛
حصلنا على صيغة الفرق بين المربعات في القوس الأول ، وفي القوس الثاني هناك عامل مشترك وهو اثنان. دعنا نطبق الصيغة ونخرج العامل المشترك.
(4 * x ^ 2 - y ^ 2) + (4 * x + 2 * y) = (2 * x - y) * (2 * x + y) + 2 * (2 * x + y) ؛
يمكن ملاحظة أنه تم الحصول على قوسين متطابقين. نخرجهم كعامل مشترك.
(2 * x - y) * (2 * x + y) + 2 * (2 * x + y) = (2 * x + y) * (2 * x - y) +2) = (2 * x + y) ) * (2 * س ص + 2) ؛
إجابه:(2 * س + ص) * (2 * س ص + 2) ؛
كما ترى ، لا توجد طريقة عالمية. مع الخبرة ، ستأتي المهارة وسيكون تحليل كثير الحدود إلى عوامل أمرًا سهلاً للغاية.