Разделы: Математика
Тип урока:
Цель: сформировать умение разложения многочлена на множители.
Задачи:
Методы работы:
Оборудование урока: интерактивная доска или кодоскоп, таблицы с формулами сокращенного умножения, инструкции, раздаточный материал для работы в группах.
Структура урока:
Ход урока
1. Организационный момент
Учитель проверяет готовность кабинета и учащихся к уроку.
2. Формулирование темы, цели и задач урока-практикума
3. Проверка домашнего задания
На доске образцы решения упражнений домашнего задания №943 (а,в); №945 (в,г). Образцы выполнены учащимися класса. (Эта группа учащихся была выявлена на предыдущем уроке, свое решение они оформили на перемене). Учащиеся готовятся провести “защиту” решений.
Учитель:
Проверяет наличие домашних заданий в тетрадях учащихся.
Предлагает учащимся класса ответить на вопрос: “Какие трудности вызвало выполнение задания?”.
Предлагает сверить свое решение с решением на доске.
Предлагает учащимся у доски ответить на вопросы, которые возникли у учащихся на местах при проверке по образцам.
Комментирует ответы учащихся, дополняет ответы, разъясняет (если это необходимо).
Подводит итоги выполнения домашнего задания.
Учащиеся:
Предъявляют домашнее задание учителю.
Меняются тетрадями (в парах) и проверяют друг у друга.
Отвечают на вопросы учителя.
Сверяют свое решение с образцами.
Выступают в роли оппонентов, вносят дополнения, исправления, записывают другой способ, если способ решения в тетради отличается от способа на доске.
Обращаются за необходимыми пояснениями к учащимся, к учителю.
Находят способы проверки полученных результатов.
Участвуют в оценке качества выполнения заданий у доски.
4. Актуализация опорных знаний и умений учащихся
1. Устная работа
Учитель:
Ответьте на вопросы:
2. На доске записаны многочлены:
1. 14х 3 – 14х 5
2. 16х 2 – (2 + х) 2
3. 9 – х 2 – 2хy – y 2
4. x 3 - 3x – 2
Учитель предлагает учащимся выполнить разложение многочленов № 1-3 на множители:
Одному ученику предлагает разложить на множители многочлен №4 (индивидуальное задание повышенной трудности, задание выполняет на формате А 4). Затем на доске появляется образец решения заданий №1-3 (выполнен учителем), образец решения задания №4 (выполнен учеником).
3. Разминка
Учитель дает указания разложить на множители и выбрать букву, связанную с правильным ответом. Сложив буквы вы получите фамилию величайшего математика ХVII века, который внес огромный вклад в развитие теории решения уравнений. (Декарт)
5. Физкультминутка Учащимся зачитываются высказывания. Если высказывание верно, то учащиеся должны поднять руки вверх, а если неверно, то присесть за парту. (Приложение 2)
6. Инструктирование по выполнению заданий практикума.
На интерактивной доске или отдельном плакате таблица с инструкцией.
При разложении многочлена на множители необходимо соблюдать следующий порядок:
1. вынести общий множитель за скобки (если он есть);
2. применить формулы сокращенного умножения (если это возможно);
3. применить способ группировки;
4. проверить полученный результат умножением.
Учитель :
Предлагает вниманию учащихся инструкцию (делает акцент на шаге 4).
Предлагает выполнение заданий практикума по группам.
Раздает рабочие листы на группы, листы с копировальной бумагой для оформления заданий в тетрадях и их последующей проверки.
Определяет время на работу в группах, на работу в тетрадях.
Учащиеся :
Читают инструкцию.
Внимательно слушают учителя.
Рассаживаются по группам (по 4-5 человек).
Готовятся к выполнению практической работы.
7. Выполнение заданий в группах
Рабочие листы с заданиями для групп. (Приложение 3)
Учитель :
Управляет самостоятельной работой в группах.
Оценивает умение работать учащихся самостоятельно, умение работать в группе, качество оформления рабочего листа.
Учащиеся :
Выполняют задания на листах с копировальной бумагой, вложенных в рабочую тетрадь.
Обсуждают способы рационального решения.
Оформляют рабочий лист от группы.
Готовятся к защите выполненной работы.
8. Проверка и обсуждение выполнения задания
На интерактивной доске ответы.
Учитель :
Собирает копии решений.
Управляет работой учащихся, отчитывающихся по рабочим листам.
Предлагает провести самооценку своих работ, сравнить ответы по тетрадям, рабочим листам и образцам на доске.
Напоминает критерии выставления отметки за работу, за участие в ее выполнении.
Дает разъяснения по возникающим вопросам решения или самооценки.
Подводит первые итоги выполнения практической работы и рефлексию.
Подводит (совместно с учащимися) итог урока.
Говорит о том, что окончательно итоги будут подведены после проверки копий работ, выполненных учащимися.
Учащиеся :
Сдают копии учителю.
Рабочие листы крепят на доске.
Отчитываются о выполнении работы.
Осуществляют самопроверку и самооценку выполнения работы.
9. Постановка домашнего задания
На доске записано домашнее задание: № 1016(а,б); 1017 (в,г); № 1021 (г,д,е)*
Учитель :
Предлагает записать обязательную часть задания на дом.
Дает комментарий к его выполнению.
Предлагает более подготовленным ученикам записать № 1021 (г,д,е)*.
Сообщает, что нужно подготовиться к следующему уроку обзорного повторения
ПЛАН-КОНСПЕКТ УРОКА
Тип урока : урок изучения нового материала на основе проблемного обучения9 Цель урока
создать условия для отработки умений и навыков разложения многочлена на множители с использованием различных способов.
10. Задачи:
Образовательные
повторить алгоритмы операций: вынесение общего множителя за скобку, способ группировки, формулы сокращённого умножения.
сформировать умение:
– применять знания по теме «разложение многочлена на множители различными способами»;
– выполнять задания по выбранному способу действия;
– выбирать наиболее рациональный способ для рационализации вычислений, преобразования многочленов.
Развивающие
способствовать развитию познавательных способностей, внимания, памяти, мышления обучающихся через применения различных упражнений;
развивать навыки самостоятельной работы и групповой работы; поддерживать интерес обучающихся к математике
Воспитывающие
поддерживать интерес обучающихся к математике
11.Формируемые УУД
Личностные: осознание цели деятельности (ожидаемый результат), осознание или выбор способа деятельности (Как я это сделаю? С помощью чего получу результат?), анализ и оценивание полученного результата; оценка своих возможностей;
Регулятивные: учитывать правило в планировании и контроле способа решения, планирование, оценка результатов работы;
Познавательные: выбор наиболее эффективных способов решения задач, структурирование знаний; преобразование информации из одного вида в другой.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, соблюдение правил речевого поведения, умение высказывать и обосновывать свою точку зрения, учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
12 .Методы:
по источникам знаний: словесные, наглядные;
относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
13.Формы работы учащихся: фронтальная, индивидуальная, групповая.
14. Необходимое техническое оборудование: компьютер, проектор, интерактивная доска, раздаточный материал (лист самоконтроля, карточки с заданиями), электронная презентация, выполненная в программе Power Point
15.Планируемые результаты :
Личностные воспитание чувства само- и взаимоуважения; развитие сотрудничества при работе в группах;
Метапредметные развитие речи; развитие у учащихся самостоятельности; развитие внимательности при поиске ошибок.
Предметные развитие умений работать с информацией, овладение способами решения
Ход урока:
1. Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания ; инструктаж по работе с листом оценивания Приложение 1 , уточнение критериев оценки.
Проверка домашнего задания и актуализация знаний
1. 3а + 6 b = 3(а + 2 b )2. 100 – 20с + с 2 = (10 + с) 2
3. с 2 – 81 = (с – 9)(с + 9)
4. 6х 3 – 5х 4 = х 4 (6х – 5)
5. ау – 3у – 4а + 12 = у(а – 3) – 4(а – 3)
6. 0,09х 2 – 0,25у 2 = (0,03х – 0,05у)(0,03х + 0,05у)
7. с(х – 3) – d (х – 3) = (х – 3)(с – d )
8. 14х 2 – 7х = 7х(7х – 1)
9. -1600 + а 12 = (40 + а 6 ) (40 - а 6 )
10. 9х 2 – 24ху + 16у 2 = (3х – 4у) 2
11. 8с 3 – 2с 2 + 4с – 1 =
2с 2 (4с – 1) + (4с – 1) = (4с – 1)2с 2
12. b 4 + с 2 – 2 b 2 с = ( b – c ) 2
(задания для домашней работы взяты из учебника, включают в себя разложение на множители разными способами. Для того, чтобы выполнить данную работу учащимся необходимо вспомнить ранее изученный материал)
Ответы, записанные на слайде, содержат ошибки, учащиеся учатся видеть способы, а так же замечая ошибки запоминают способы действий,
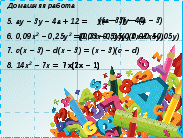

Учащиеся в группах, проверив домашнее задание выставляют баллы за проделанную работу
2 Эстафета Приложение 2 (участники команд, по очереди выполняют задание, при этом стрелкой соединяют пример и способ его разложения)
3a – 12b = 3(а – 4 b)2a + 2b + a 2 + ab = (а + b) (2 + а)
9a 2 – 16b 2 = ( 3а – 4 b)(3a + 4b)
16a 2 - 8ab + b 2 = (4а – b) 2
7a 2 b – 14ab 2 + 7ab = 7ab(a – 2b + 1)
a 2 + ab- a – ac- bc + c = (a + b – 1)(a – c)
25a 2 + 70ab+ 49b 2 = ( 5а + 7 b) 2
5х 2 – 45у 2 = 5(х – 3у)(х + 3у)
![]()
Не раскладывается на множители
Метод группировки

С помощью слайда проводится проверка проделанной работы, при этом обращается внимание на то, что последний пример нужно соединить с двумя способами разложения (вынесение за скобку общего множителя и формула сокращенного умножения)
Учащиеся оценивают проделанную работу, вносят результаты в листы оценивания, а так же формулируют тему урока

3. Выполнение заданий (учащимся предлагается выполнить задание. Обсуждая решение в группе ребята приходят к выводу, что для разложения данных многочленов на множители требуется несколько способов. Та команда, которая первая предложит верное разложение, имеет право на доске записать свое решение, остальные записывают его в тетради.. В команде налажена работа помощи учащимся, которым тяжело справиться с заданием)
1) 2a 2 - 2b 25) 5m 2 + 5n 2 – 10mn
9) 84 – 42y – 7xy + 14x
13) x 2 y + 14xy 2 + 49y 3
2) 3a 2 + 6ab + 3b 2
6) cx 2 – cy 2
10) -7b 2 – 14bc – 7c 2
14) 3ab 2 – 27a
3) x 3 – 4x
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8a 3 b + 56a 2 b 2 – 98ab 3
4) 3ab + 15b – 3a – 15
8) x 4 – x 2
12) c 4 - 81
16) 0 , 09t 4 – t 6
4. Заключительный этап –Разложение многочлена на множители
Вынесение общего множителя за скобки
Метод группировки
Формула сокращенного умножения
Итог урока. Учащиеся отвечают на вопросы: Какую задачу мы ставили? Удалось решить нам поставленную задачу? Каким способом? Какие получили результаты? Какими способами раскладывается многочлен на множители? Для выполнения каких заданий можно применить эти знания? Что на уроке у вас хорошо получалось? Над чем еще нужно поработать?
В течение урока учащиеся оценивали себя, в конце урока им предлагается сложить полученные баллы и выставить оценку в соответствии с предложенной шкалой.
Заключительное слово учителя: Сегодня на уроке мы учились определять какие способы необходимо применить, чтобы разложить многочлены на множители. Для закрепления проделанной работы
Домашнее задание: §19, №708, №710
Дополнительное задание:
Решите уравнение х 3 + 4х 2 = 9х + 36
Понятия "многочлен" и "разложение многочлена на множители" по алгебре встречаются очень часто, ведь их необходимо знать, чтобы с легкостью производить вычисления c большими многозначными числами. В этой статье будет описано несколько способов разложения. Все они достаточно просты в применении, стоит лишь правильно подобрать нужный в каждом конкретном случае.
Многочлен является суммой одночленов, то есть выражений, содержащих только операцию умножения.
Например, 2 * x * y - это одночлен, а вот 2 * x * y + 25 - многочлен, который состоит из 2 одночленов: 2 * x * y и 25. Такие многочлены называет двучленами.
Иногда для удобства решения примеров с многозначными значениями выражение необходимо преобразовать, например, разложить на некоторое количество множителей, то есть чисел или выражений, между которыми производится действие умножения. Есть ряд способов разложения многочлена на множители. Стоит рассмотреть их начиная с самого примитивного, который применяют еще в начальных классах.

Формула разложения многочлена на множители способом группировки в общем виде выглядит таким образом:
ac + bd + bc + ad = (ac + bc) + (ad + bd)
Необходимо сгруппировать одночлены так, чтобы в каждой группе появился общий множитель. В первой скобке это множитель с, а во второй - d. Это нужно сделать для того, чтобы затем вынести его за скобку, тем самым упростив вычисления.
Простейший пример разложения многочлена на множители способом группировки приведен ниже:
10ас + 14bc - 25a - 35b = (10ас - 25а) + (14bc - 35b)
В первую скобку нужно взять слагаемые с множителем а, который и будет общим, а во вторую - со множителем b. Обратите внимание на знаки + и - в готовом выражении. Мы ставим перед одночленом тот знак, который был в начальном выражении. То есть нужно работать не с выражением 25а, а с выражением -25. Знак минус как бы «приклеить» к стоящему за ним выражению и всегда учитывать его при вычислениях.
На следующем шаге нужно вынести множитель, который является общим, за скобку. Именно для этого и делается группировка. Вынести за скобку - значит выписать перед скобкой (опуская знак умножения) все те множители, которые с точностью повторяются во всех слагаемых, которые находятся в скобке. Если в скобке не 2, а 3 слагаемых и больше, общий множитель должен содержаться в каждом из них, иначе его нельзя вынести за скобку.
В нашем случае - только по 2 слагаемых в скобках. Общий множитель сразу виден. В первой скобке - это а, во второй - b. Здесь нужно обратить внимание на цифровые коэффициенты. В первой скобке оба коэффициента (10 и 25) кратны 5. Это значит, что можно вынести за скобку не только а, но и 5а. Перед скобкой выписать 5а, а затем каждое из слагаемых в скобках поделить на общий множитель, который был вынесен, и также записать частное в скобках, не забывая о знаках + и - Со второй скобкой поступить также, вынести 7b, так как и 14 и 35 кратно 7.
10ас + 14bc - 25a - 35b = (10ас - 25а) + (14bc - 35b) = 5а(2c - 5) + 7b(2c - 5).
Получилось 2 слагаемых: 5а(2c - 5) и 7b(2c - 5). Каждое из них содержит общий множитель (все выражение в скобках здесь совпадает, значит, является общим множителем): 2с - 5. Его тоже нужно вынести за скобку, то есть во второй скобке остаются слагаемые 5а и 7b:
5а(2c - 5) + 7b(2c - 5) = (2c - 5)*(5а + 7b).
Итак, полное выражение:
10ас + 14bc - 25a - 35b = (10ас - 25а) + (14bc - 35b) = 5а(2c - 5) + 7b(2c - 5) = (2c - 5)*(5а + 7b).
Таким образом, многочлен 10ас + 14bc - 25a - 35b раскладываается на 2 множителя: (2c - 5) и (5а + 7b). Знак умножения между ними при записи можно опускать

Иногда встречаются выражения такого типа: 5а 2 + 50а 3 , здесь можно вынести за скобку не только а или 5а, а даже 5а 2 . Всегда нужно стараться вынести максимально большой общий множитель за скобку. В нашем случае, если разделить каждое слагаемое на общий множитель, то получается:
5а 2 / 5а 2 = 1; 50а 3 / 5а 2 = 10а (при вычислении частного нескольких степеней с равными основаниями основание сохраняется, а показатель степени вычитается). Таким образом, в скобке остается единица (ни в коем случае не забывайте писать единицу, если выносите за скобку целиком одно из слагаемых) и частное от деления: 10а. Получается, что:
5а 2 + 50а 3 = 5а 2 (1 + 10а)
Для удобства вычислений были выведены несколько формул. Они называются формулами сокращенного умножения и используются довольно часто. Эти формулы помогают разложить на множители многочлены, содержащие степени. Это еще один действенный способ разложения на множители. Итак, вот они:

Вычисления по ним производятся достаточно просто. Например:
Действия по формуле квадрата разности производятся аналогично этим. Остается формула разность квадратов. Примеры на эту формулу очень легко определить и найти среди других выражений. Например:
Важно, чтобы каждое из слагаемых являлось квадратом какого-либо выражения. Тогда этот многочлен подлежит разложению на множители по формуле разности квадратов. Для этого не обязательно, чтобы над числом стояла именно вторая степень. Встречаются многочлены, содежащие большие степени, но все равно подходящие к этим формулам.
a 8 +10a 4 +25 = (a 4) 2 + 2*a 4 *5 + 5 2 = (a 4 +5) 2
В данном примере а 8 можно представить как (a 4) 2 , то есть квадрат некого выражения. 25 - это 5 2 , а 10а 4 - это удвоенное произведениеслагаемых2*a 4 *5. То есть данное выражение, несмотря на наличие степеней с большими показателями, можно разложить на 2 множителя, чтобы в последствии работать с ними.
Такие же формулы существуют для разложения на множители многочленов, содержащих кубы. Они немного посложнее тех, что с квадратами:
Последние две формулы практически не испольуются с целью разложения многочлена на множители, так как они сложны, и достаточно редко встречаются многочлены, полностью соответствующие именно такому строению, чтобы их можно было разложить по этим формулам. Но их все равно нужно знать, так как они потребуются при действиях в обратном направлении - при раскрытии скобок.

Рассмотрим пример: 64a 3 − 8b 3 = (4a) 3 − (2b) 3 = (4a − 2b)((4a) 2 + 4a*2b + (2b) 2) = (4a−2b)(16a 2 + 8ab + 4b 2).
Здесь взяты достаточно простые числа, поэтому сразу можно увидеть, что 64а 3 - это (4а) 3 , а 8b 3 - это (2b) 3 . Таким образом, этот многочлен раскладывается по формуле разность кубов на 2 множителя. Действия по формуле суммы кубов производятся по аналогии.
Важно понимать, что далеко не все многочлены подлежат разложению хотя бы одним из способов. Но есть такие выражения, которые содержат большие степени, чем квадрат или куб, но их также можно разложить по формуам сокращенного умножения. Например: x 12 + 125y 3 =(x 4) 3 +(5y) 3 =(x 4 +5y)*((x 4) 2 − x 4 *5y+(5y) 2)=(x 4 + 5y)(x 8 − 5x 4 y + 25y 2).
В этом примере содержится аж 12 степень. Но даже его возможно разложить на множители по формуле суммы кубов. Для этого нужно представить х 12 как (x 4) 3 , то есть как куб какого-либо выражения. Теперь в формулу вместо а нужно подставлять именно его. Ну а выражение 125у 3 - это куб 5у. Далее следует составить произведение по формуле и произвести вычисления.

На первых порах или в случае возникших сомнений, вы всегда можете произвести проверку обратным умножением. Вам нужно лишь раскрыть скобки в получившемся выражении и выполнить действия с подобными слагаемыми. Этот метод относится ко всем перечисленным способам сокращения: как к работе с общим множителем и группировке, так и к действиям по формулам кубов и квадратных степеней.
Многочлены являются важнейшим типом математических выражений. На основе многочленов построено множество уравнений, неравенств, функций. Задачи различного уровня сложности зачастую содержат этапы разностороннего преобразования многочленов. Так как математически любой полином представляет собой алгебраическую сумму нескольких одночленов, наиболее кардинальным и нужным изменением является преобразования ряда многочлена в произведение двух (или более) множителей. В уравнениях, обладающих возможностью обнуления одной из частей, перевод полинома на множители позволяет приравнять какую-то часть к нулю, и решить, таким образом, все уравнение.
Предыдущие видеоуроки показали нам, что в линейной алгебре существует три основных способа перевода многочленов в множители. Это вынесение общего множителя за скобки, перегруппировка по подобным членам, применение формул сокращенного умножения. Если все члены полинома обладают некой общей основой, то её легко можно вынести за скобки, оставив остатки от делений в виде измененного многочлена в скобках. Но чаще всего, один множитель не подходит под все одночлены, затрагивая лишь их часть. При этом, другая часть мономов может иметь свою общую основу. В таких случаях применяется способ группировки - по сути говоря, вынесение за скобки нескольких множителей, и создание комплексного выражения, которое можно преобразовать другими путями. И, наконец, существует целый комплекс специальных формул. Все они образованы абстрактными расчетами, использующими метод простейшего почленного переумножения. В ходе расчетов, многие элементы в начальном выражении сокращаются, оставляя небольшие многочлены. Что бы каждый раз не проводить емкие вычисления, можно применять готовые формулы, их обратные варианты, или обобщенные выводы этих формул.

На практике, часто бывает так, что в одном упражнении приходится комбинировать несколько приемов, в том числе, и из разряда преобразования многочленов. Рассмотрим пример. Разложить на множители бином:
Выносим общий множитель 3х за скобки:
3х3 - 3ху2 = 3х(х2 - у2)
Как можно заметить на видео, вторые скобки содержат разность квадратов. Применяем обратную формулу сокращенного умножения, получая:
3х(х2 - у2) = 3х(х + у)(х - у)
Другой пример. Преобразуем выражение вида:
18а2 - 48а + 32
Уменьшаем числовые коэффициенты, вынося за скобки двойку:
18а2 - 48а + 32 = 2(9а2 - 24а + 16)

Что бы найти подходящую формулу сокращенного умножения для данного случая, необходимо несколько скорректировать выражение, подогнав под условия формулы:
2(9а2 - 24а + 16) = 2((3а)2 - 2(3а)4 + (4)2)
Порой, формулу в запутанном выражении увидеть не так просто. Приходится применять методы разложения выражения на составляющие элементы, или добавлять мнимые пары конструкций, типа +х-х. Корректируя выражение, мы должны соблюдать правила преемственности знаков, и сохранности значения выражения. При этом, нужно стараться привести многочлен к полному соответствию с абстрактным вариантом формулы. По нашему примеру применяем формулу квадрата разности:
2((3а)2 - 2(3а)4 + (4)2) = 2(3а - 4)
Решим более сложное упражнение. Разложим на множители многочлен:
У3 - 3у2 + 6у - 8
Для начала, проведем удобную группировку - первый и четвертый элемент в одну группу, второй и третий - во вторую:
У3 - 3у2 + 6у - 8 = (у3 - 8) - (3у2 - 6у)
Обратим внимание, что знаки во вторых скобках сменились на противоположные, так как мы вынесли минус за пределы выражения. В первых скобках можем записать так:
(у3 - (2)3) - (3у2 - 6у)
Это позволяет применить формулу сокращенного умножения для нахождения разности кубов:
(у3 - (2)3) - (3у2 - 6у) = (у - 2)(у2 + 2у + 4) - (3у2 - 6у)

Выносим со вторых скобок общий множитель 3у, после чего, выносим из всего выражения (бинома) скобки (у - 2), приводим подобные слагаемые:
(у - 2)(у2 + 2у + 4) - (3у2 - 6у) = (у - 2)(у2 + 2у + 4) - 3у(у - 2) =
= (у - 2)(у2 + 2у + 4 - 3у) = (у - 2)(у2 - у + 4)
В общем приближении, существует определенный алгоритм действий при решении подобных упражнений.
1. Ищем общие множители для всего выражения;
2. Группируем подобные одночлены, ищем общие множители для них;
3. Стараемся вынести за скобки наиболее подходящее выражение;
4. Применяем формулы сокращенного умножения;
5. Если на каком-то этапе процесс не идет - вписываем мнимую пару выражений вида -х+х, или иные самоаннулирующиеся конструкции;
6. Приводим подобные слагаемые, сокращаем лишние элементы
Все пункты алгоритма редко когда применимы в одном задании, но общий ход решения любого упражнения по теме можно соблюдать в заданном порядке.
Существует несколько различных способов разложения многочлена на множители. Чаще всего на практике применяется не один, а сразу несколько способов. Какого-то определенного порядка действий тут быть не может, в каждом примере все индивидуально. Но можно пробывать придерживаться следующего порядка:
1. Если есть общий множитель, то вынести его за скобку;
2. После этого попробовать разложить многочлен на множители, используя формулы сокращенного умножения;
3. Если после этого мы еще не получили необходимого результата, следует попытаться воспользоваться способом группировки.
1. a^2 - b^2 = (a+b)*(a-b);
2. (a+b)^2 = a^2+2*a*b+b^2;
3. (a-b)^2 = a^2-2*a*b+b^2;
4. a^3+b^3 = (a+b)*(a^2 - a*b+b^2);
5. a^3 - b^3 = (a-b)*(a^2 + a*b+b^2);
Теперь для закрепления разберем несколько примеров:
Пример 1.
Разложить многочлен на множители: (a^2+1)^2 - 4*a^2
Сначала применим формулу сокращенного умножения «разность квадратов» и раскроем внутренние скобки.
(a^2+1)^2 - 4*a^2 = ((a^2+1)-2*a)*((a^2+1)+2*a) = (a^2+1-2*a)*(a^2+1+2*a);
Заметим, что в скобках получились выражения для квадрата суммы и квадрата разности двух выражений. Применим их и получаем ответ.
a^2+1-2*a)*(a^2+1+2*a) = (a-1)^2*(a+1)^2;
Ответ: (a-1)^2*(a+1)^2;
Пример 2.
Разложить многочлен 4*x^2 - y^2 + 4*x +2*y на множители.
Как видим напрямую здесь никакой из способов не подходит. Но есть два квадрата, их можно сгруппировать. Попробуем.
4*x^2 - y^2 + 4*x +2*y = (4*x^2 - y^2) +(4*x +2*y);
Получили в первой скобке формулу разности квадратов, А во второй скобке есть общий множитель двойка. Применим формулу и вынесем общий множитель.
(4*x^2 - y^2) +(4*x +2*y)= (2*x - y)*(2*x+y) +2*(2*x+y);
Видно, что получились две одинаковые скобки. Вынесем их как общий множитель.
(2*x - y)*(2*x+y) +2*(2*x+y) = (2*x+y)*(2*x - y)+2)= (2*x+y)*(2*x-y+2);
Ответ: (2*x+y)*(2*x-y+2);
Как видите, универсального способа нет. С опытом придет навык и раскладывать многочлен на множители будет очень легко.