Sezioni: Matematica
Tipo di lezione:
Obbiettivo: formare la capacità di fattorizzare un polinomio.
Compiti:
Metodi di lavoro:
Attrezzatura per le lezioni: lavagna interattiva o cannocchiale, tabelle con formule di moltiplicazione abbreviate, istruzioni, dispense per lavori di gruppo.
Struttura della lezione:
Durante le lezioni
1. Momento organizzativo
L'insegnante controlla la disponibilità della classe e degli studenti per la lezione.
2. Formulazione dell'argomento, scopi e obiettivi della lezione-pratica
3. Controllo dei compiti
Alla lavagna ci sono esempi di risoluzione degli esercizi n. 943 (a, c); 945 (c, d). I campioni sono stati realizzati dagli studenti della classe. (Questo gruppo di studenti è stato individuato nella lezione precedente, hanno formalizzato la loro decisione durante la ricreazione). Gli studenti si preparano a “difendere” le soluzioni.
Insegnante:
Controlla i compiti nei quaderni degli studenti.
Invita gli studenti della classe a rispondere alla domanda: “Quali difficoltà ha causato il compito?”.
Si offre di confrontare la loro soluzione con la soluzione sulla lavagna.
Invita gli studenti alla lavagna a rispondere alle domande che gli studenti avevano sul campo durante il controllo dei campioni.
Commenta le risposte degli studenti, integra le risposte, spiega (se necessario).
Riassume i compiti.
Studenti:
Presenta i compiti all'insegnante.
Cambia i quaderni (a coppie) e controlla tra loro.
Rispondi alle domande dell'insegnante.
Controlla la tua soluzione con campioni.
Agiscono come avversari, apportano aggiunte, correzioni, annotano un metodo diverso se il metodo di soluzione nel quaderno è diverso dal metodo sulla lavagna.
Chiedere le spiegazioni necessarie agli studenti, al docente.
Trova modi per controllare i risultati.
Partecipa alla valutazione della qualità dei compiti alla lavagna.
4. Aggiornare le conoscenze e le abilità di base degli studenti
1. Lavoro orale
Insegnante:
Rispondi alle domande:
2. I polinomi sono scritti alla lavagna:
1. 14x 3 - 14x 5
2. 16x 2 - (2 +x) 2
3. 9 - x 2 - 2xy - y 2
4.x3 - 3x - 2
Insegnante invita gli studenti a fattorizzare i polinomi n. 1-3:
A uno studente viene offerto di fattorizzare il polinomio n. 4 (un compito individuale di maggiore difficoltà, il compito viene svolto sul formato A 4). Quindi una soluzione campione per i compiti n. 1-3 (fatto dall'insegnante), una soluzione campione per il compito n. 4 (fatto dallo studente) appare alla lavagna.
3. Riscaldati
L'insegnante dà istruzioni per fattorizzare e scegliere la lettera associata alla risposta corretta. Aggiungendo le lettere otterrai il nome del più grande matematico del 17° secolo, che diede un enorme contributo allo sviluppo della teoria della risoluzione delle equazioni. (Cartesio)
5. Educazione fisica Gli studenti leggono le dichiarazioni. Se l'affermazione è vera, allora gli studenti dovrebbero alzare le mani e, se non è vera, sedersi alla scrivania. (Allegato 2)
6. Istruzioni su come completare i compiti dell'officina.
Su una lavagna interattiva o su un poster separato, un tavolo con le istruzioni.
Quando si scompone un polinomio in fattori, è necessario osservare il seguente ordine:
1. mettere fuori parentesi il fattore comune (se presente);
2. applicare formule di moltiplicazione abbreviate (se possibile);
3. applicare il metodo di raggruppamento;
4. verificare il risultato ottenuto moltiplicando.
Insegnante:
Offre istruzioni agli studenti (enfatizza il passaggio 4).
Offre l'implementazione di incarichi di workshop in gruppi.
Distribuisce fogli di lavoro in gruppi, fogli con carta carbone per il completamento dei compiti in quaderni e la loro successiva verifica.
Determina il tempo per il lavoro in gruppo, per il lavoro nei taccuini.
studenti:
Hanno letto le istruzioni.
Gli insegnanti ascoltano attentamente.
Sono seduti in gruppi (4-5 persone ciascuno).
Prepararsi per il lavoro pratico.
7. Esecuzione di compiti in gruppo
Fogli di lavoro con compiti per gruppi. (Allegato 3)
Insegnante:
Gestisce il lavoro autonomo in gruppo.
Valuta la capacità degli studenti di lavorare in modo indipendente, la capacità di lavorare in gruppo, la qualità della progettazione del foglio di lavoro.
studenti:
Eseguire attività su fogli di carta carbone racchiusi in una cartella di lavoro.
Discutere soluzioni razionali.
Preparare un foglio di lavoro per il gruppo.
Preparati a difendere il tuo lavoro.
8. Verifica e discussione dell'incarico
Risposte alla lavagna.
Insegnante:
Raccoglie copie delle decisioni.
Gestisce il lavoro degli studenti che riportano sui fogli di lavoro.
Si offre di condurre un'autovalutazione del proprio lavoro, confrontare le risposte in quaderni, fogli di lavoro ed esempi alla lavagna.
Richiama i criteri per la valutazione del lavoro, per la partecipazione alla sua attuazione.
Fornisce chiarimenti sulle decisioni emergenti o sui problemi di autovalutazione.
Riassume i primi risultati del lavoro pratico e della riflessione.
Riassume (insieme agli studenti) la lezione.
Dice che i risultati finali saranno riassunti dopo aver controllato le copie del lavoro svolto dagli studenti.
studenti:
Dare copie all'insegnante.
I fogli di lavoro sono allegati alla lavagna.
Reportistica sull'esecuzione del lavoro.
Eseguire l'autovalutazione e l'autovalutazione delle prestazioni lavorative.
9. Impostazione dei compiti
I compiti sono scritti alla lavagna: n. 1016 (a, b); 1017 (c, d); N. 1021 (d, e, f)*
Insegnante:
Si offre di annotare la parte obbligatoria dell'incarico a casa.
Fa un commento sulla sua attuazione.
Invita gli studenti più preparati a scrivere n. 1021 (d, e, f) *.
Ti dice di prepararti per la prossima lezione di riesame
PIANO DI LEZIONI
Tipo di lezione : apprendimento delle lezioni nuovo materiale basato sull'apprendimento basato sui problemi9 Scopo della lezione
creare le condizioni per esercitare le abilità e le capacità di fattorizzazione di un polinomio utilizzando vari metodi.
10. Compiti:
Educativo
ripetere gli algoritmi delle operazioni: togliere dalla parentesi il fattore comune, metodo di raggruppamento, formule di moltiplicazione abbreviate.
costruire abilità:
– applicare le conoscenze sull'argomento "fattorizzazione di un polinomio in vari modi";
– svolgere compiti secondo il metodo di azione scelto;
– scegli il modo più razionale per razionalizzare i calcoli, trasformare i polinomi.
Educativo
promuovere lo sviluppo delle capacità cognitive, dell'attenzione, della memoria, del pensiero degli studenti attraverso l'uso di vari esercizi;
sviluppare capacità lavoro indipendente e lavoro di gruppo; mantenere gli studenti interessati alla matematica
educatori
mantenere gli studenti interessati alla matematica
11.UUD sagomato
Personale: consapevolezza dello scopo dell'attività (risultato atteso), consapevolezza o scelta del metodo di attività (Come lo farò? Come otterrò il risultato?), analisi e valutazione del risultato; valutazione delle proprie capacità;
Regolamentazione: tenere conto della regola nella pianificazione e nel controllo del modo di risolvere, pianificare, valutare i risultati del lavoro;
cognitivo: selezione dei più modi efficaci problem solving, strutturazione della conoscenza;convertire le informazioni da un modulo all'altro.
Comunicativo: pianificazionecooperazione educativa con l'insegnante e i coetanei, rispetto delle regole del comportamento vocale, capacità di esprimere esostanziare il proprio punto di vista, tenere conto di opinioni diverse e sforzarsi di coordinare le varie posizioni in cooperazione.
12. Metodi:
per fonti di conoscenza: verbale, visiva;
sulla natura dell'attività cognitiva: riproduttiva, parzialmente esplorativa.
13. Forme di lavoro degli studenti: frontale, individuale, di gruppo.
14. Necessario Equipaggiamento tecnico: computer, proiettore, lavagna interattiva, dispense (foglio di autocontrollo, schede attività), presentazione elettronica realizzata nel programmapotenzapunto
15. Risultati pianificati :
Personale promuovere un senso di autostima e rispetto reciproco; sviluppo della cooperazione quando si lavora in gruppo;
Metasoggetto sviluppo del linguaggio; sviluppo dell'indipendenza degli studenti; sviluppo dell'attenzione nella ricerca di errori.
materia sviluppo delle competenze per lavorare con le informazioni, padronanza delle soluzioni
Durante le lezioni:
1. Salutare gli studenti. Verifica della disponibilità della classe per la lezione da parte dell'insegnante; organizzazione dell'attenzione; esercitazione sulla scheda di valutazioneallegato 1 , affinamento dei criteri di valutazione.
Controllo dei compiti e aggiornamento delle conoscenze
1. 3a + 6b= 3(a + 2b)2. 100 - 20s + s 2 = (10 + s) 2
3. con 2 - 81 \u003d (s - 9) (s + 9)
4. 6x 3 – 5 volte 4 = x 4 (6x - 5)
5. ay - 3y - 4a + 12 \u003d y (a - 3) - 4 (a - 3)
6. 0,09x 2 - 0,25 anni 2 \u003d (0,03x - 0,05y) (0,03x + 0,05y)
7. c (x - 3) -d(x - 3) \u003d (x - 3) (s -d)
8. 14x 2 - 7x \u003d 7x (7x - 1)
9. -1600 + a 12 = (40 + a 6 ) (40 - a 6 )
10,9x 2 – 24 anni + 16 anni 2 = (3x - 4 anni) 2
11.8s 3 – 2s 2 + 4 secondi - 1 =
2s 2 (4s - 1) + (4s - 1) = (4s - 1)2s 2
12. b 4 + con 2 – 2 b 2 c = (b – c) 2
(compiti a casa presi dal libro di testo, includono la fattorizzazione in vari modi. Per completare questo lavoro Gli studenti devono ricordare ciò che hanno imparato finora
Le risposte registrate sulla diapositiva contengono errori, gli studenti imparano a vedere i modi e inoltre, notando gli errori, ricordano i modi di agire,
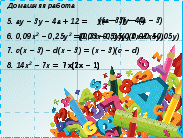

Gli studenti in gruppo, dopo aver controllato i compiti, assegnano punti per il lavoro svolto.
2 RelèAllegato 2 (i membri del team, a turno, completano l'attività, mentre la freccia collega l'esempio e il modo in cui è scomposto)
3a-12b = 3(a – 4 b)2a + 2b + a 2 +ab = (un + b) (2+a)
9a 2 – 16 ter 2 = ( 3a - 4 b)(3a + 4b)
16 bis 2 - 8ab+b 2 = (4à – b) 2
7a 2 b-14ab 2 + 7ab = 7ab(a - 2b + 1)
un 2 + ab- a - ac- bc + c = (a + b - 1) (a - c)
25 bis 2 + 70 ab + 49 b 2 = ( 5a + 7 b) 2
5 volte 2 - 45 anni 2 \u003d 5 (x - 3y) (x + 3y)
![]()
Non fattorizza
Metodo di raggruppamento

Con l'aiuto della diapositiva si verifica il lavoro svolto e si richiama l'attenzione sul fatto che l'ultimo esempio deve essere combinato con due metodi di scomposizione (tra parentesi il fattore comune e la formula di moltiplicazione abbreviata)
Gli studenti valutano il lavoro svolto, inseriscono i risultati nelle schede di valutazione e formulano anche l'argomento della lezione.

3. Completamento dei compiti (gli studenti sono invitati a completare il compito. Discutendo la soluzione in un gruppo, i ragazzi giungono alla conclusione che sono necessari diversi modi per fattorizzare questi polinomi. Il team che per primo offre la scomposizione corretta ha il diritto di annotare la loro soluzione alla lavagna, il resto la scrivi su un quaderno. Il team ha stabilito un lavoro per aiutare gli studenti che hanno difficoltà a far fronte al compito)
1) 2a 2 - 2b 25) 5m 2 + 5n 2 – 10 minuti
9) 84 - 42 anni - 7 anni + 14 anni
13) X 2 y+14xy 2 + 49 anni 3
2) 3a 2 + 6ab + 3b 2
6) cx 2 – ci 2
10) -7b 2 – 14bc – 7c 2
14) 3ab 2 – 27 bis
3) X 3 – 4x
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8 bis 3 b+56a 2 b 2 – 98ab 3
4) 3ab + 15b - 3a - 15
8) X 4 - X 2
12) c 4 - 81
16) 0 , 09t 4 - t 6
4. La fase finale –Fattorizzazione di un polinomio
Togliendo il fattore comune da parentesi
Metodo di raggruppamento
Formula di moltiplicazione abbreviata
Riassunto della lezione. Gli studenti rispondono alle domande:Quale compito ci siamo prefissati? Siamo riusciti a risolvere il nostro problema? Come? Quali sono stati i risultati? Come si può fattorizzare un polinomio? Per quali compiti può essere applicata questa conoscenza? Cosa hai fatto bene a lezione? Cos'altro deve essere lavorato?
Durante la lezione gli studenti si autovalutano, al termine della lezione viene chiesto di sommare i punteggi e dare una valutazione secondo la scala proposta.
Ultima parola dell'insegnante: Oggi nella lezione abbiamo imparato a determinare quali metodi devono essere applicati per fattorizzare i polinomi. Per consolidare il lavoro svolto
Compiti a casa: §19, #708, #710
Compito aggiuntivo:
Risolvi l'equazione x 3 + 4x 2 = 9x + 36
I concetti di "polinomio" e "fattorizzazione di un polinomio" in algebra sono molto comuni, perché è necessario conoscerli per eseguire facilmente calcoli con grandi numeri multivalore. Questo articolo descriverà diversi metodi di scomposizione. Tutti sono abbastanza semplici da usare, devi solo scegliere quello giusto in ogni caso.
Un polinomio è la somma di monomi, cioè espressioni contenenti solo l'operazione di moltiplicazione.
Ad esempio, 2 * x * y è un monomio, ma 2 * x * y + 25 è un polinomio, che consiste di 2 monomi: 2 * x * y e 25. Tali polinomi sono chiamati binomi.
A volte, per comodità di risolvere esempi con valori multivalore, l'espressione deve essere trasformata, ad esempio, scomposta in un certo numero di fattori, cioè numeri o espressioni tra i quali viene eseguita l'operazione di moltiplicazione. Esistono diversi modi per fattorizzare un polinomio. Vale la pena considerarli partendo dal più primitivo, che viene utilizzato anche nelle classi primarie.

La formula per scomporre un polinomio in fattori con il metodo di raggruppamento in generale è simile alla seguente:
ac + bd + bc + ad = (ac + bc) + (ad + bd)
È necessario raggruppare i monomi in modo che appaia un fattore comune in ciascun gruppo. Nella prima parentesi, questo è il fattore c, e nella seconda - d. Questo va fatto per poi estrarlo dalla parentesi, semplificando così i calcoli.
L'esempio più semplice di scomposizione in fattori di un polinomio utilizzando il metodo di raggruppamento è riportato di seguito:
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b)
Nella prima parentesi, devi prendere i termini con il fattore a, che sarà comune, e nella seconda, con il fattore b. Presta attenzione ai segni + e - nell'espressione finita. Mettiamo davanti al monomio il segno che era nell'espressione iniziale. Cioè, devi lavorare non con l'espressione 25a, ma con l'espressione -25. Il segno meno, per così dire, è "incollato" all'espressione dietro di esso e ne tiene sempre conto nei calcoli.
Nel passaggio successivo, è necessario eliminare il fattore, che è comune, fuori dalla parentesi. Ecco a cosa serve il raggruppamento. Toglierlo dalla parentesi significa trascrivere prima della parentesi (omettendo il segno di moltiplicazione) tutti quei fattori che si ripetono esattamente in tutti i termini che sono nella parentesi. Se nella parentesi non ci sono 2, ma 3 o più termini, il fattore comune deve essere contenuto in ciascuno di essi, altrimenti non può essere tolto dalla parentesi.
Nel nostro caso, solo 2 termini tra parentesi. Il moltiplicatore complessivo è immediatamente visibile. La prima parentesi è a, la seconda è b. Qui è necessario prestare attenzione ai coefficienti digitali. Nella prima parentesi, entrambi i coefficienti (10 e 25) sono multipli di 5. Ciò significa che non solo a, ma anche 5a possono essere racchiusi tra parentesi. Prima della parentesi, scrivi 5a, quindi dividi ciascuno dei termini tra parentesi per il fattore comune che è stato eliminato, e annota anche il quoziente tra parentesi, senza dimenticare i segni + e -. Fai lo stesso con la seconda parentesi , elimina 7b, poiché 14 e 35 multiplo di 7.
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b) = 5a (2c - 5) + 7b (2c - 5).
Si sono rivelati 2 termini: 5a (2c - 5) e 7b (2c - 5). Ognuno di essi contiene un fattore comune (l'intera espressione tra parentesi qui è la stessa, il che significa che è un fattore comune): 2c - 5. Deve anche essere tolto dalla parentesi, cioè i termini 5a e 7b rimangono nella seconda fascia:
5a(2c - 5) + 7b(2c - 5) = (2c - 5)*(5a + 7b).
Quindi l'espressione completa è:
10ac + 14bc - 25a - 35b \u003d (10ac - 25a) + (14bc - 35b) \u003d 5a (2c - 5) + 7b (2c - 5) \u003d (2c - 5) * (5a + 7b).
Pertanto, il polinomio 10ac + 14bc - 25a - 35b è scomposto in 2 fattori: (2c - 5) e (5a + 7b). Il segno di moltiplicazione tra di loro può essere omesso durante la scrittura

A volte ci sono espressioni di questo tipo: 5a 2 + 50a 3, qui puoi mettere tra parentesi non solo a o 5a, ma anche 5a 2. Dovresti sempre cercare di togliere dalla parentesi il più grande fattore comune possibile. Nel nostro caso, se dividiamo ciascun termine per un fattore comune, otteniamo:
5a 2 / 5a 2 = 1; 50a 3 / 5a 2 = 10a(quando si calcola il quoziente di più potenze con basi uguali, si conserva la base e si sottrae l'esponente). Così si resta tra parentesi (in nessun caso non dimenticarsi di scriverne una se si estrae interamente dalla parentesi uno dei termini) e il quoziente di divisione: 10a. Si scopre che:
5a 2 + 50a 3 = 5a 2 (1 + 10a)
Per comodità di calcolo, sono state derivate diverse formule. Sono chiamate formule di moltiplicazione ridotte e sono usate abbastanza spesso. Queste formule aiutano a fattorizzare i polinomi contenenti poteri. È un altro modo effettivo fattorizzazione. Quindi eccoli qui:

I calcoli su di essi sono fatti in modo molto semplice. Per esempio:
Le operazioni secondo la formula del quadrato della differenza vengono eseguite in modo simile a queste. Ciò che rimane è la formula della differenza dei quadrati. Esempi di questa formula sono molto facili da identificare e trovare tra le altre espressioni. Per esempio:
È importante che ciascuno dei termini sia il quadrato di qualche espressione. Quindi questo polinomio deve essere scomposto dalla formula della differenza dei quadrati. Per questo, non è necessario che la seconda potenza sia superiore al numero. Esistono polinomi contenenti grandi potenze, ma comunque adatti a queste formule.
a 8 +10a 4 +25 = (a 4) 2 + 2*a 4 *5 + 5 2 = (a 4 +5) 2
A questo esempio e 8 può essere rappresentato come (a 4) 2 , cioè il quadrato di una certa espressione. 25 è 5 2 e 10a è 4 - questo è il doppio prodotto dei termini 2*a 4 *5. Cioè, questa espressione, nonostante la presenza di gradi con esponenti grandi, può essere scomposta in 2 fattori per poter lavorare con loro in seguito.
Le stesse formule esistono per la fattorizzazione di polinomi contenenti cubi. Sono un po' più complicati di quelli con i quadrati:
Le ultime due formule non vengono praticamente utilizzate allo scopo di fattorizzare un polinomio, poiché sono complesse, ed è abbastanza raro trovare polinomi che corrispondano completamente proprio a tale struttura in modo che possano essere scomposti secondo queste formule. Ma devi ancora conoscerli, poiché saranno necessari per azioni nella direzione opposta, quando si aprono le parentesi.

Considera un esempio: 64a 3 − 8b 3 = (4a) 3 − (2b) 3 = (4a − 2b)((4a) 2 + 4a*2b + (2b) 2) = (4a−2b)(16a 2 + 8ab + 4b 2 ).
Abbiamo preso qui numeri abbastanza primi, quindi puoi immediatamente vedere che 64a 3 è (4a) 3 e 8b 3 è (2b) 3 . Pertanto, questo polinomio viene ampliato dalla formula differenza dei cubi in 2 fattori. Le azioni sulla formula della somma dei cubi vengono eseguite per analogia.
È importante capire che non tutti i polinomi possono essere scomposti in almeno uno dei modi. Ma ci sono tali espressioni che contengono poteri più grandi di un quadrato o di un cubo, ma possono anche essere espanse in forme di moltiplicazione abbreviate. Ad esempio: x 12 + 125y 3 =(x 4) 3 +(5y) 3 =(x 4 +5y)*((x 4) 2 − x 4 *5y+(5y) 2)=(x 4 + 5y) ( x 8 − 5x 4 y + 25 y 2).
Questo esempio contiene fino a 12 gradi. Ma anche esso può essere scomposto usando la formula della somma dei cubi. Per fare ciò, devi rappresentare x 12 come (x 4) 3, cioè come un cubo di qualche espressione. Ora, invece di a, devi sostituirlo nella formula. Bene, l'espressione 125y 3 è il cubo di 5y. Il prossimo passo è scrivere la formula ed eseguire i calcoli.

All'inizio, o in caso di dubbio, puoi sempre controllare per moltiplicazione inversa. Devi solo aprire le parentesi nell'espressione risultante ed eseguire azioni con termini simili. Questo metodo si applica a tutti i metodi di riduzione di cui sopra: sia per lavorare con un fattore comune e raggruppamento, sia per operazioni sulle formule dei cubi e delle potenze quadrate.
I polinomi sono il tipo più importante di espressioni matematiche. Sulla base dei polinomi è stato costruito un insieme di equazioni, disequazioni e funzioni. Problemi di vari livelli di complessità spesso contengono fasi di trasformazione versatile dei polinomi. Poiché matematicamente qualsiasi polinomio è una somma algebrica di più monomi, il cambiamento più fondamentale e necessario è la trasformazione di una serie di polinomi in un prodotto di due (o più) fattori. Nelle equazioni che hanno la capacità di azzerare una delle parti, la traduzione del polinomio in fattori consente di uguagliare una parte a zero, e quindi risolvere l'intera equazione.
I precedenti video tutorial ci hanno mostrato che nell'algebra lineare ci sono tre modi principali per tradurre i polinomi in fattori. Questo è togliere il fattore comune tra parentesi, raggruppare secondo termini simili, usando formule di moltiplicazione abbreviate. Se tutti i membri del polinomio hanno una base comune, allora può essere facilmente tolto dalle parentesi, lasciando tra parentesi il resto delle divisioni sotto forma di un polinomio modificato. Ma molto spesso, un fattore non si adatta a tutti i monomi, interessando solo una parte di essi. In questo caso, l'altra parte dei monomi può avere una propria base comune. In questi casi, viene utilizzato un metodo di raggruppamento, ovvero mettendo tra parentesi diversi fattori e creando un'espressione complessa che può essere trasformata in altri modi. E, infine, c'è un intero complesso di formule speciali. Tutti sono formati da calcoli astratti utilizzando il metodo della più semplice moltiplicazione termine per termine. Durante i calcoli, molti elementi nell'espressione iniziale vengono ridotti, lasciando piccoli polinomi. Per non eseguire calcoli capienti ogni volta, puoi utilizzare formule già pronte, le loro varianti inverse o conclusioni generalizzate di queste formule.

In pratica capita spesso che in un esercizio si debbano combinare più tecniche, comprese quelle della categoria delle trasformazioni polinomiali. Considera un esempio. Fattorizzare per binomio:
Prendiamo tra parentesi il fattore comune 3:
3x3 - 3x2 = 3x(x2 - y2)
Come puoi vedere nel video, le seconde parentesi contengono la differenza dei quadrati. Applichiamo la formula della moltiplicazione abbreviata inversa, ottenendo:
3x(x2 - y2) = 3x(x + y)(x - y)
Un altro esempio. Trasformiamo un'espressione della forma:
18a2 - 48a + 32
Riduciamo i coefficienti numerici mettendo tra parentesi il due:
18a2 - 48a + 32 = 2(9a2 - 24a + 16)

Per trovare una formula di moltiplicazione abbreviata adatta per questo caso, è necessario aggiustare leggermente l'espressione adattando la formula alle condizioni:
2(9a2 - 24a + 16) = 2((3a)2 - 2(3a)4 + (4)2)
A volte, una formula in un'espressione confusa non è così facile da vedere. Si devono applicare i metodi per scomporre l'espressione nei suoi elementi costitutivi, o aggiungere coppie immaginarie di costruzioni, come +x-x. Correggendo l'espressione, dobbiamo rispettare le regole della successione dei segni e la conservazione del significato dell'espressione. Allo stesso tempo, si dovrebbe cercare di portare il polinomio alla piena conformità con la versione astratta della formula. Nel nostro esempio applichiamo la formula del quadrato della differenza:
2((3a)2 - 2(3a)4 + (4)2) = 2(3a - 4)
Facciamo un esercizio più difficile. Fattorizziamo il polinomio:
U3 - 3y2 + 6y - 8
Per cominciare, eseguiamo un raggruppamento conveniente - il primo e il quarto elemento in un gruppo, il secondo e il terzo - nel secondo:
Y3 - 3y2 + 6y - 8 = (y3 - 8) - (3y2 - 6y)
Si noti che i segni nelle seconde parentesi sono stati invertiti, poiché abbiamo spostato il meno dall'espressione. Tra le prime parentesi possiamo scrivere:
(y3 - (2)3) - (3y2 - 6y)
Questo ti permette di applicare la formula di moltiplicazione ridotta per trovare la differenza di cubi:
(y3 - (2)3) - (3y2 - 6y) = (y - 2) (y2 + 2y + 4) - (3y2 - 6y)

Rimuoviamo il fattore comune 3y dalla seconda parentesi, dopodiché togliamo le parentesi (y - 2) dall'intera espressione (binomio), diamo termini simili:
(y - 2)(y2 + 2y + 4) - (3y2 - 6y) = (y - 2)(y2 + 2y + 4) - 3y(y - 2) =
\u003d (y - 2) (y2 + 2y + 4 - 3y) \u003d (y - 2) (y2 - y + 4)
In un'approssimazione generale, esiste un certo algoritmo di azioni quando si risolvono tali esercizi.
1. Cerchiamo fattori comuni per l'intera espressione;
2. Raggruppiamo monomi simili, cerchiamo fattori comuni per loro;
3. Cerchiamo di mettere tra parentesi l'espressione più appropriata;
4. Applichiamo le formule della moltiplicazione abbreviata;
5. Se a un certo punto il processo non va, entriamo in una coppia immaginaria di espressioni della forma -x + x, o altre costruzioni auto-cancellanti;
6. Diamo termini simili, riduciamo gli elementi non necessari
Tutti i punti dell'algoritmo sono raramente applicabili in un'attività, ma il corso generale per risolvere qualsiasi esercizio su un argomento può essere seguito in un determinato ordine.
Esiste diversi modi fattorizzazione di un polinomio. Molto spesso, in pratica, non vengono utilizzati uno, ma diversi metodi contemporaneamente. Non può esserci un ordine specifico di azioni qui, in ogni esempio tutto è individuale. Ma puoi provare a seguire il seguente ordine:
1. Se esiste un fattore comune, estrarlo dalla parentesi;
2. Successivamente, prova a fattorizzare il polinomio usando le formule di moltiplicazione abbreviate;
3. Se dopo non abbiamo ancora ricevuto il risultato desiderato, dovremmo provare a utilizzare il metodo di raggruppamento.
1. a^2 - b^2 = (a+b)*(a-b);
2. (a+b)^2 = a^2+2*a*b+b^2;
3. (a-b)^2 = a^2-2*a*b+b^2;
4. a^3+b^3 = (a+b)*(a^2 - a*b+b^2);
5. a^3 - b^3 = (a-b)*(a^2 + a*b+b^2);
Ora diamo un'occhiata ad alcuni esempi:
Esempio 1
Fattorizzare il polinomio: (a^2+1)^2 - 4*a^2
Innanzitutto, applichiamo la formula di moltiplicazione abbreviata "differenza di quadrati" e apriamo le parentesi interne.
(a^2+1)^2 - 4*a^2 = ((a^2+1)-2*a)*((a^2+1)+2*a) = (a^2+1 -2*a)*(a^2+1+2*a);
Si noti che le espressioni per il quadrato della somma e il quadrato della differenza di due espressioni si ottengono tra parentesi. Applicali e ottieni la risposta.
a^2+1-2*a)*(a^2+1+2*a) = (a-1)^2*(a+1)^2;
Risposta:(a-1)^2*(a+1)^2;
Esempio 2
Fattorizzare il polinomio 4*x^2 - y^2 + 4*x +2*y.
Come puoi vedere direttamente qui, nessuno dei metodi è adatto. Ma ci sono due quadrati, possono essere raggruppati. Proviamo.
4*x^2 - y^2 + 4*x +2*y = (4*x^2 - y^2) +(4*x +2*y);
Abbiamo la formula per la differenza dei quadrati nella prima parentesi, e nella seconda parentesi c'è un fattore comune di due. Applichiamo la formula ed eliminiamo il fattore comune.
(4*x^2 - y^2) +(4*x +2*y)= (2*x - y)*(2*x+y) +2*(2*x+y);
Si può notare che si ottengono due parentesi identiche. Li prendiamo come un fattore comune.
(2*x - y)*(2*x+y) +2*(2*x+y) = (2*x+y)*(2*x - y)+2)= (2*x+ y )*(2*x-y+2);
Risposta:(2*x+y)*(2*x-y+2);
Come puoi vedere, non esiste un modo universale. Con l'esperienza, l'abilità arriverà e scomporre il polinomio in fattori sarà molto facile.