Sections: Mathématiques
Type de leçon :
Cible: forment la capacité de factoriser un polynôme.
Tâches:
Les méthodes de travail:
Matériel de cours : tableau blanc interactif ou rétroprojecteur, tableaux avec formules de multiplication abrégées, instructions, polycopié pour le travail en groupe.
Structure de la leçon :
Pendant les cours
1. Moment organisationnel
L'enseignant vérifie l'état de préparation de la classe et des élèves pour la leçon.
2. Formulation du sujet, des buts et des objectifs de la leçon-pratique
3. Vérification des devoirs
Au tableau figurent des exemples de résolution d'exercices de devoirs n ° 943 (a, c); N° 945 (c, d). Les échantillons ont été réalisés par les élèves de la classe. (Ce groupe d'élèves a été identifié dans la leçon précédente, ils ont formalisé leur décision à la récréation). Les élèves se préparent à « défendre » les solutions.
Prof:
Vérifie les devoirs dans les cahiers des élèves.
Invite les élèves de la classe à répondre à la question : « Quelles difficultés le devoir a-t-il causé ? ».
Propose de comparer sa solution avec la solution au tableau.
Invite les élèves au tableau noir à répondre aux questions que les élèves se sont posées sur le terrain lors de la vérification des échantillons.
Il commente les réponses des élèves, complète les réponses, explique (si nécessaire).
Résume les devoirs.
Étudiants:
Présenter les devoirs au professeur.
Changez de cahiers (par paires) et vérifiez les uns avec les autres.
Répondez aux questions du professeur.
Vérifiez votre solution avec des échantillons.
Ils agissent comme des adversaires, font des ajouts, des corrections, notent une méthode différente si la méthode de résolution dans le cahier diffère de la méthode au tableau.
Demander les explications nécessaires aux élèves, au professeur.
Trouvez des moyens de vérifier les résultats.
Participer à l'évaluation de la qualité des tâches au tableau noir.
4. Mettre à jour les connaissances et compétences de base des étudiants
1. Travail oral
Prof:
Répondez aux questions:
2. Les polynômes sont écrits au tableau :
1. 14x 3 - 14x 5
2. 16x 2 - (2 + x) 2
3. 9 - x 2 - 2xy - y 2
4.x3 - 3x - 2
Prof invite les élèves à factoriser les polynômes n° 1 à 3 :
Un étudiant se voit proposer de factoriser le polynôme n° 4 (une tâche individuelle de difficulté accrue, la tâche est réalisée sur le format A 4). Ensuite, un exemple de solution pour les tâches n ° 1 à 3 (faites par l'enseignant), un exemple de solution pour la tâche n ° 4 (faite par l'élève) apparaît au tableau.
3. Échauffez-vous
L'enseignant donne des instructions pour factoriser et choisir la lettre associée à la bonne réponse. En ajoutant les lettres, vous obtiendrez le nom du plus grand mathématicien du 17ème siècle, qui a apporté une énorme contribution au développement de la théorie de la résolution des équations. (Descartes)
5. Education physique Les élèves lisent les énoncés. Si l'affirmation est vraie, alors les élèves doivent lever la main, et si ce n'est pas vrai, alors s'asseoir au bureau. (Annexe 2)
6. Instruction sur la façon d'accomplir les tâches de l'atelier.
Sur un tableau blanc interactif ou une affiche séparée, un tableau avec des instructions.
Lors de la décomposition d'un polynôme en facteurs, l'ordre suivant doit être respecté :
1. mettre le facteur commun entre parenthèses (s'il y en a);
2. appliquer des formules de multiplication abrégées (si possible) ;
3. appliquer la méthode de regroupement ;
4. vérifier le résultat obtenu par multiplication.
Prof:
Offre des instructions aux élèves (met l'accent sur l'étape 4).
Propose la mise en œuvre de travaux d'ateliers en groupe.
Distribue des feuilles de travail en groupes, des feuilles avec du papier carbone pour effectuer des devoirs dans des cahiers et leur vérification ultérieure.
Détermine le temps pour le travail en groupe, pour le travail dans les cahiers.
étudiants:
Ils lisent les consignes.
Les professeurs écoutent attentivement.
Ils sont assis en groupe (4-5 personnes chacun).
Préparez-vous aux travaux pratiques.
7. Effectuer des tâches en groupe
Feuilles de travail avec des tâches pour les groupes. (Annexe 3)
Prof:
Gère le travail indépendant en groupe.
Évalue la capacité des étudiants à travailler de manière autonome, la capacité à travailler en groupe, la qualité de la conception de la feuille de travail.
étudiants:
Effectuer des tâches sur des feuilles de papier carbone jointes dans un classeur.
Discutez des solutions rationnelles.
Préparez une feuille de travail pour le groupe.
Préparez-vous à défendre votre travail.
8. Vérification et discussion du devoir
Réponses sur le tableau blanc.
Prof:
Recueille des copies des décisions.
Gère le travail des étudiants qui rapportent sur des feuilles de travail.
Propose de procéder à une auto-évaluation de son travail, de comparer les réponses dans des cahiers, des feuilles de travail et des échantillons au tableau.
Rappelle les critères de notation pour le travail, pour la participation à sa mise en œuvre.
Fournit des éclaircissements sur les questions émergentes de décision ou d'auto-évaluation.
Résume les premiers résultats de travaux pratiques et de réflexion.
Résume (avec les élèves) la leçon.
Dit que les résultats finaux seront résumés après vérification des copies des travaux effectués par les étudiants.
étudiants:
Donnez des copies à l'enseignant.
Les feuilles de travail sont jointes au tableau.
Rapport sur l'exécution des travaux.
Effectuer une auto-évaluation et une auto-évaluation de la performance au travail.
9. Définir les devoirs
Les devoirs sont écrits au tableau: n ° 1016 (a, b); 1017 (c, d); N° 1021 (d, e, f)*
Prof:
Propose d'écrire la partie obligatoire de la mission à la maison.
Donne un commentaire sur sa mise en œuvre.
Invite les étudiants plus préparés à écrire le n ° 1021 (d, e, f) *.
Vous dit de vous préparer pour la prochaine leçon de révision
PLAN DE COURS
Type de leçon : leçon d'apprentissage nouveau matériel basé sur l'apprentissage par problèmes9 Objectif de la leçon
créer des conditions pour pratiquer les compétences et les capacités de factorisation d'un polynôme à l'aide de diverses méthodes.
10. Tâches :
Éducatif
répéter les algorithmes des opérations : sortie du facteur commun hors de la parenthèse, méthode de regroupement, formules de multiplication abrégées.
développer des compétences :
– appliquer les connaissances sur le thème "factorisation d'un polynôme de différentes manières" ;
– effectuer des tâches selon le mode d'action choisi;
– choisir la manière la plus rationnelle de rationaliser les calculs, transformer des polynômes.
Éducatif
favoriser le développement des capacités cognitives, de l'attention, de la mémoire, de la réflexion des élèves grâce à l'utilisation de divers exercices;
Développer les compétences travail indépendant et travail de groupe; maintenir l'intérêt des élèves pour les mathématiques
éducateurs
maintenir l'intérêt des élèves pour les mathématiques
11.UUD en forme
Personnel: prise de conscience du but de l'activité (résultat attendu), prise de conscience ou choix de la méthode d'activité (Comment vais-je le faire ? Comment vais-je obtenir le résultat ?), analyse et évaluation du résultat ; évaluation de leurs capacités;
Réglementaire : prendre en compte la règle dans la planification et le contrôle de la manière de résoudre, de planifier, d'évaluer les résultats du travail;
Cognitif: sélection des plus moyens efficaces résolution de problèmes, structuration des connaissances ;convertir des informations d'un formulaire à un autre.
Communicatif: Planificationcoopération éducative avec l'enseignant et les pairs, respect des règles de comportement de la parole, capacité d'expression etétayer leur point de vue, tenir compte des avis divergents et s'efforcer de coordonner les différentes positions dans la coopération.
12 .Méthodes :
par sources de connaissances : verbales, visuelles ;
concernant la nature de l'activité cognitive : reproductrice, partiellement exploratoire.
13. Formes de travail étudiant : frontale, individuelle, collective.
14. Nécessaire Equipement technique: ordinateur, projecteur, tableau blanc interactif, polycopiés (fiche d'autocontrôle, cartes à tâches), présentation électronique faite dans le programmePuissanceindiquer
15.Résultats prévus :
Personnel favoriser un sentiment de respect de soi et de respect mutuel; développement de la coopération lors du travail en groupe;
Métasujet développement de la parole; le développement de l'autonomie des étudiants ; développement de l'attention lors de la recherche d'erreurs.
matière développement des compétences pour travailler avec l'information, maîtrise des solutions
Pendant les cours :
1. Accueillir les élèves. Vérification de l'état de préparation de la classe pour la leçon par l'enseignant; organisation de l'attention; fiche d'évaluation tutorielPièce jointe 1 , affinement des critères d'évaluation.
Vérification des devoirs et mise à jour des connaissances
1. 3a + 6b= 3(a + 2b)2. 100 - 20s + s 2 = (10 + s) 2
3. avec 2 - 81 \u003d (s - 9) (s + 9)
4. 6x 3 – 5x 4 =x 4 (6x - 5)
5. ay - 3a - 4a + 12 \u003d a (a - 3) - 4 (a - 3)
6. 0,09x 2 - 0.25y 2 \u003d (0,03x - 0,05y) (0,03x + 0,05y)
7. c (x - 3) -ré(x - 3) \u003d (x - 3) (s -ré)
8. 14x 2 - 7x \u003d 7x (7x - 1)
9. -1600 + un 12 = (40 + un 6 ) (40 - un 6 )
10,9x 2 – 24xy + 16y 2 = (3x - 4a) 2
11.8s 3 – 2s 2 + 4s - 1 =
2s 2 (4s - 1) + (4s - 1) = (4s - 1)2s 2
12. b 4 + avec 2 – 2 b 2 c = (b – c) 2
(les devoirs tirés du manuel, incluent la factorisation de diverses manières. Afin de compléter ce travail Les élèves doivent se rappeler ce qu'ils ont appris jusqu'à présent
Les réponses enregistrées sur la diapositive contiennent des erreurs, les élèves apprennent à voir des façons, et aussi, en remarquant des erreurs, se souviennent des façons d'agir,
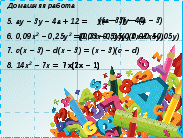

Les élèves en groupes, après avoir vérifié leurs devoirs, attribuent des points pour le travail effectué.
2 RelaisAnnexe 2 (les membres de l'équipe accomplissent la tâche à tour de rôle, tandis que la flèche relie l'exemple et la façon dont il est décomposé)
3a-12b = 3(a – 4 b)2a + 2b + une 2 + ab = (un + b) (2 + un)
9a 2 – 16b 2 = ( 3a - 4 b)(3a + 4b)
16a 2 - 8ab+b 2 = (4à – b) 2
7a 2 b-14ab 2 + 7ab = 7ab(a - 2b + 1)
un 2 + ab- une - ac- bc + c = (a + b - 1)(a - c)
25a 2 + 70ab + 49b 2 = ( 5a + 7 b) 2
5x 2 - 45 ans 2 \u003d 5 (x - 3a) (x + 3a)
![]()
Ne se factorise pas
Méthode de regroupement

À l'aide de la diapositive, le travail effectué est vérifié et l'attention est attirée sur le fait que le dernier exemple doit être combiné avec deux méthodes de décomposition (la mise entre parenthèses du facteur commun et la formule de multiplication abrégée)
Les élèves évaluent le travail effectué, inscrivent les résultats dans les feuilles d'évaluation et formulent également le sujet de la leçon.

3. Réaliser des tâches (les élèves sont invités à terminer la tâche. En discutant de la solution en groupe, les gars arrivent à la conclusion que plusieurs façons sont nécessaires pour factoriser ces polynômes. L'équipe qui propose la décomposition correcte a le droit d'écrire leur solution au tableau, le reste l'écrit dans un cahier.. L'équipe a mis en place des travaux pour aider les élèves qui ont du mal à faire face à la tâche)
1) 2a 2 - 2b 25) 5m 2 + 5n 2 – 10mn
9) 84 - 42a - 7xy + 14x
13) X 2 y+14xy 2 + 49a 3
2) 3a 2 + 6ab + 3b 2
6) cx 2 – cy 2
10) -7b 2 – 14bc – 7c 2
14) 3ab 2 – 27a
3) X 3 – 4x
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8a 3 b+56a 2 b 2 – 98ab 3
4) 3ab + 15b - 3a - 15
8) X 4 - X 2
12) c 4 - 81
16) 0 , 09t 4 – t 6
4. L'étape finale –Factoriser un polynôme
Sortir le facteur commun des parenthèses
Méthode de regroupement
Formule de multiplication abrégée
Résumé de la leçon. Les élèves répondent aux questions :Quelle tâche nous sommes-nous fixés ? Avons-nous pu résoudre notre problème ? Comment? Quels ont été les résultats ? Comment factoriser un polynôme ? Pour quelles tâches ces connaissances peuvent-elles être appliquées ? Qu'est-ce que tu as bien fait en classe ? Sur quoi d'autre faut-il travailler ?
Pendant la leçon, les élèves s'évaluent eux-mêmes, à la fin de la leçon, il leur est demandé d'additionner les notes et de donner une appréciation conformément au barème proposé.
Dernier mot de l'enseignant : Aujourd'hui, dans la leçon, nous avons appris à déterminer quelles méthodes doivent être appliquées pour factoriser des polynômes. Pour consolider le travail accompli
Devoirs : §19, #708, #710
Tâche supplémentaire :
Résoudre l'équation x 3 + 4x 2 = 9x + 36
Les concepts de "polynôme" et de "factorisation d'un polynôme" en algèbre sont très courants, car il faut les connaître pour effectuer facilement des calculs avec de grands nombres multivalués. Cet article décrira plusieurs méthodes de décomposition. Tous sont assez simples à utiliser, il vous suffit de choisir le bon dans chaque cas.
Un polynôme est la somme de monômes, c'est-à-dire des expressions contenant uniquement l'opération de multiplication.
Par exemple, 2 * x * y est un monôme, mais 2 * x * y + 25 est un polynôme composé de 2 monômes : 2 * x * y et 25. Ces polynômes sont appelés binômes.
Parfois, pour la commodité de résoudre des exemples avec des valeurs multivaluées, l'expression doit être transformée, par exemple, décomposée en un certain nombre de facteurs, c'est-à-dire des nombres ou des expressions entre lesquels l'opération de multiplication est effectuée. Il existe plusieurs façons de factoriser un polynôme. Cela vaut la peine de les considérer à partir du plus primitif, qui est utilisé même dans les classes primaires.

La formule pour factoriser un polynôme en facteurs par la méthode de regroupement ressemble en général à ceci :
ac + bd + bc + ad = (ac + bc) + (ad + bd)
Il faut regrouper les monômes pour qu'un facteur commun apparaisse dans chaque groupe. Dans la première parenthèse, c'est le facteur c, et dans la seconde - d. Cela doit être fait afin de le sortir ensuite du support, simplifiant ainsi les calculs.
L'exemple le plus simple de factorisation d'un polynôme en facteurs à l'aide de la méthode de regroupement est donné ci-dessous :
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b)
Dans la première tranche, vous devez prendre les termes avec le facteur a, qui sera commun, et dans la seconde - avec le facteur b. Faites attention aux signes + et - dans l'expression finie. On place devant le monôme le signe qui était dans l'expression initiale. Autrement dit, vous devez travailler non pas avec l'expression 25a, mais avec l'expression -25. Le signe moins, pour ainsi dire, est «collé» à l'expression derrière et en tient toujours compte dans les calculs.
À l'étape suivante, vous devez retirer le facteur, qui est commun, du support. C'est à cela que sert le regroupement. Le retirer de la parenthèse signifie écrire avant la parenthèse (en omettant le signe de multiplication) tous les facteurs qui se répètent exactement dans tous les termes qui sont dans la parenthèse. S'il n'y a pas 2, mais 3 termes ou plus dans la parenthèse, le facteur commun doit être contenu dans chacun d'eux, sinon il ne peut pas être retiré de la parenthèse.
Dans notre cas, seulement 2 termes entre parenthèses. Le multiplicateur global est immédiatement visible. La première parenthèse est a, la seconde est b. Ici, vous devez faire attention aux coefficients numériques. Dans la première parenthèse, les deux coefficients (10 et 25) sont des multiples de 5. Cela signifie que non seulement a, mais aussi 5a peuvent être mis entre parenthèses. Avant la parenthèse, écrivez 5a, puis divisez chacun des termes entre parenthèses par le facteur commun qui a été retiré, et notez également le quotient entre parenthèses, sans oublier les signes + et -. Faites de même avec la deuxième parenthèse , enlevez 7b, puisque 14 et 35 multiple de 7.
10ac + 14bc - 25a - 35b = (10ac - 25a) + (14bc - 35b) = 5a (2c - 5) + 7b (2c - 5).
Il s'est avéré 2 termes : 5a (2c - 5) et 7b (2c - 5). Chacun d'eux contient un facteur commun (l'ensemble de l'expression entre parenthèses ici est la même, ce qui signifie qu'il s'agit d'un facteur commun) : 2c - 5. Il faut également le sortir de la parenthèse, c'est-à-dire les termes 5a et 7b reste dans la seconde tranche :
5a(2c - 5) + 7b(2c - 5) = (2c - 5)*(5a + 7b).
Donc l'expression complète est :
10ac + 14bc - 25a - 35b \u003d (10ac - 25a) + (14bc - 35b) \u003d 5a (2c - 5) + 7b (2c - 5) \u003d (2c - 5) * (5a + 7b).
Ainsi, le polynôme 10ac + 14bc - 25a - 35b se décompose en 2 facteurs : (2c - 5) et (5a + 7b). Le signe de multiplication entre eux peut être omis lors de l'écriture

Il existe parfois des expressions de ce type : 5a 2 + 50a 3, ici vous pouvez mettre entre parenthèses non seulement a ou 5a, mais même 5a 2. Vous devriez toujours essayer de retirer le plus grand facteur commun possible de la fourchette. Dans notre cas, si nous divisons chaque terme par un diviseur commun, nous obtenons :
5a 2 / 5a 2 = 1 ; 50a 3 / 5a 2 = 10a(lors du calcul du quotient de plusieurs puissances avec des bases égales, la base est conservée et l'exposant est soustrait). Ainsi, on reste entre parenthèses (n'oubliez en aucun cas d'en écrire un si vous sortez entièrement un des termes de la parenthèse) et le quotient de division : 10a. Il se trouve que:
5a 2 + 50a 3 = 5a 2 (1 + 10a)
Pour la commodité des calculs, plusieurs formules ont été dérivées. Elles sont appelées formules de multiplication réduite et sont utilisées assez souvent. Ces formules aident à factoriser les polynômes contenant des puissances. C'est un autre façon efficace factorisations. Alors les voici :

Les calculs sur eux sont faits assez simplement. Par exemple:
Les opérations selon la formule du carré de la différence sont effectuées de manière similaire à celles-ci. Ce qui reste est la formule de la différence des carrés. Les exemples de cette formule sont très faciles à identifier et à trouver parmi d'autres expressions. Par exemple:
Il est important que chacun des termes soit le carré d'une expression. Ensuite, ce polynôme doit être factorisé par la formule de la différence des carrés. Pour cela, il n'est pas nécessaire que la seconde puissance soit au-dessus du nombre. Il existe des polynômes contenant de grandes puissances, mais toujours adaptés à ces formules.
une 8 +10a 4 +25 = (une 4) 2 + 2*une 4 *5 + 5 2 = (une 4 +5) 2
À cet exemple et 8 peut être représenté par (a 4) 2 , c'est-à-dire le carré d'une certaine expression. 25 vaut 5 2 et 10a vaut 4 - c'est le double produit des termes 2*a 4 *5. C'est-à-dire que cette expression, malgré la présence de degrés avec de grands exposants, peut être décomposée en 2 facteurs afin de travailler avec eux plus tard.
Les mêmes formules existent pour factoriser des polynômes contenant des cubes. Ils sont un peu plus compliqués que ceux avec des carrés :
Les deux dernières formules ne sont pratiquement pas utilisées dans le but de factoriser un polynôme, car elles sont complexes, et il est assez rare de trouver des polynômes qui correspondent exactement à une telle structure pour pouvoir être décomposés selon ces formules. Mais vous devez toujours les connaître, car ils seront nécessaires pour les actions dans le sens opposé - lors de l'ouverture des parenthèses.

Prenons un exemple : 64a 3 − 8b 3 = (4a) 3 − (2b) 3 = (4a − 2b)((4a) 2 + 4a*2b + (2b) 2) = (4a−2b)(16a 2 + 8ab + 4b 2 ).
Nous avons pris des nombres assez premiers ici, donc vous pouvez immédiatement voir que 64a 3 est (4a) 3 et 8b 3 est (2b) 3 . Ainsi, ce polynôme est développé par la formule différence de cubes en 2 facteurs. Les actions sur la formule de la somme des cubes sont effectuées par analogie.
Il est important de comprendre que tous les polynômes ne peuvent pas être décomposés d'au moins une des manières. Mais il existe de telles expressions qui contiennent des puissances plus grandes qu'un carré ou un cube, mais elles peuvent également être développées en formes de multiplication abrégées. Par exemple : x 12 + 125y 3 =(x 4) 3 +(5y) 3 =(x 4 +5y)*((x 4) 2 − x 4 *5y+(5y) 2)=(x 4 + 5y) ( x 8 − 5x 4 y + 25y 2).
Cet exemple contient jusqu'à 12 degrés. Mais même cela peut être factorisé en utilisant la formule de la somme des cubes. Pour ce faire, vous devez représenter x 12 comme (x 4) 3, c'est-à-dire comme un cube d'une expression. Maintenant, au lieu de a, vous devez le remplacer dans la formule. Eh bien, l'expression 125y 3 est le cube de 5y. L'étape suivante consiste à écrire la formule et à faire les calculs.

Au début, ou en cas de doute, vous pouvez toujours vérifier par multiplication inverse. Il vous suffit d'ouvrir les crochets dans l'expression résultante et d'effectuer des actions avec des termes similaires. Cette méthode s'applique à toutes les méthodes de réduction ci-dessus: à la fois pour travailler avec un facteur commun et un groupement, et pour les opérations sur les formules des cubes et des puissances carrées.
Les polynômes sont le type le plus important d'expressions mathématiques. Sur la base de polynômes, un ensemble d'équations, d'inégalités et de fonctions a été construit. Les problèmes de différents niveaux de complexité contiennent souvent des étapes de transformation polyvalente de polynômes. Puisque mathématiquement tout polynôme est une somme algébrique de plusieurs monômes, le changement le plus fondamental et le plus nécessaire est la transformation d'une série de polynômes en un produit de deux facteurs (ou plus). Dans les équations qui ont la capacité de réinitialiser l'une des parties, la traduction du polynôme en facteurs vous permet d'assimiler une partie à zéro, et ainsi de résoudre l'équation entière.
Les didacticiels vidéo précédents nous ont montré qu'en algèbre linéaire, il existe trois façons principales de traduire des polynômes en facteurs. C'est sortir le facteur commun des parenthèses, le regrouper selon des termes similaires, en utilisant des formules de multiplication abrégées. Si tous les membres du polynôme ont une base commune, alors il peut être facilement retiré des parenthèses, laissant le reste des divisions sous la forme d'un polynôme modifié entre parenthèses. Mais le plus souvent, un facteur ne correspond pas à tous les monômes, n'affectant qu'une partie d'entre eux. Dans ce cas, l'autre partie des monômes peut avoir sa propre base commune. Dans de tels cas, une méthode de regroupement est utilisée - en fait, mettant entre parenthèses plusieurs facteurs et créant une expression complexe qui peut être transformée d'autres manières. Et, enfin, il y a tout un complexe de formules spéciales. Tous sont formés par des calculs abstraits utilisant la méthode de la multiplication terme à terme la plus simple. Lors des calculs, de nombreux éléments de l'expression initiale sont réduits, laissant de petits polynômes. Afin de ne pas effectuer de calculs volumineux à chaque fois, vous pouvez utiliser des formules toutes faites, leurs versions inverses ou des conclusions généralisées de ces formules.

En pratique, il arrive souvent que dans un exercice on doive combiner plusieurs techniques, dont celles de la catégorie des transformations polynomiales. Prenons un exemple. Factoriser par binôme :
Nous retirons le facteur commun 3 entre parenthèses :
3x3 - 3x2 = 3x(x2 - y2)
Comme vous pouvez le voir dans la vidéo, les deuxièmes parenthèses contiennent la différence des carrés. Nous appliquons la formule de multiplication abrégée inverse, obtenant :
3x(x2 - y2) = 3x(x + y)(x - y)
Un autre exemple. Transformons une expression de la forme :
18a2 - 48a + 32
Nous réduisons les coefficients numériques en mettant entre parenthèses le deux :
18a2 - 48a + 32 = 2(9a2 - 24a + 16)

Afin de trouver une formule de multiplication abrégée appropriée pour ce cas, il est nécessaire d'ajuster légèrement l'expression en ajustant la formule aux conditions :
2(9a2 - 24a + 16) = 2((3a)2 - 2(3a)4 + (4)2)
Parfois, une formule dans une expression déroutante n'est pas si facile à voir. Il faut appliquer les méthodes de décomposition de l'expression en ses éléments constitutifs, ou ajouter des paires imaginaires de constructions, telles que +x-x. En corrigeant l'expression, il faut respecter les règles de succession des signes, et la préservation du sens de l'expression. En même temps, il faut essayer de rendre le polynôme totalement conforme à la version abstraite de la formule. Dans notre exemple, nous appliquons la formule du carré de la différence :
2((3a)2 - 2(3a)4 + (4)2) = 2(3a - 4)
Faisons un exercice plus difficile. Factorisons le polynôme :
U3 - 3a2 + 6a - 8
Pour commencer, procédons à un regroupement pratique - les premier et quatrième éléments dans un groupe, les deuxième et troisième - dans le second:
A3 - 3a2 + 6a - 8 = (a3 - 8) - (3a2 - 6a)
Notez que les signes entre les deuxièmes parenthèses ont été inversés, puisque nous avons retiré le moins de l'expression. Dans les premières parenthèses, on peut écrire :
(a3 - (2)3) - (3a2 - 6a)
Cela vous permet d'appliquer la formule de multiplication réduite pour trouver la différence de cubes :
(a3 - (2)3) - (3a2 - 6a) = (a - 2) (a2 + 2a + 4) - (3a2 - 6a)

Nous retirons le facteur commun 3y des deuxièmes parenthèses, après quoi nous retirons les parenthèses (y - 2) de l'expression entière (binôme), nous donnons des termes similaires :
(y - 2)(y2 + 2y + 4) - (3y2 - 6y) = (y - 2)(y2 + 2y + 4) - 3y(y - 2) =
\u003d (y - 2) (y2 + 2y + 4 - 3y) \u003d (y - 2) (y2 - y + 4)
Dans une approximation générale, il existe un certain algorithme d'actions lors de la résolution de tels exercices.
1. Nous recherchons des facteurs communs pour toute l'expression ;
2. Nous regroupons les monômes similaires, recherchons des facteurs communs pour eux ;
3. Nous essayons de mettre entre parenthèses l'expression la plus appropriée ;
4. On applique les formules de multiplication abrégée ;
5. Si, à un moment donné, le processus ne se déroule pas, nous entrons dans une paire imaginaire d'expressions de la forme -x + x, ou d'autres constructions auto-annulantes ;
6. Nous donnons des termes similaires, réduisons les éléments inutiles
Tous les points de l'algorithme sont rarement applicables dans une tâche, mais le cours général de résolution de tout exercice sur un sujet peut être suivi dans un ordre donné.
Existe plusieurs manières différentes factorisation d'un polynôme. Le plus souvent, dans la pratique, non pas une, mais plusieurs méthodes sont utilisées à la fois. Il ne peut y avoir d'ordre spécifique d'actions ici, dans chaque exemple tout est individuel. Mais vous pouvez essayer de suivre l'ordre suivant :
1. S'il y a un facteur commun, retirez-le du support ;
2. Après cela, essayez de factoriser le polynôme en utilisant les formules de multiplication abrégées ;
3. Si après cela nous n'avons pas encore reçu le résultat souhaité, nous devrions essayer d'utiliser la méthode de regroupement.
1. a^2 - b^2 = (a+b)*(a-b);
2. (a+b)^2 = a^2+2*a*b+b^2 ;
3. (a-b)^2 = a^2-2*a*b+b^2 ;
4. a^3+b^3 = (a+b)*(a^2 - a*b+b^2) ;
5. a^3 - b^3 = (a-b)*(a^2 + a*b+b^2) ;
Voyons maintenant quelques exemples :
Exemple 1
Factorisez le polynôme : (a^2+1)^2 - 4*a^2
Tout d'abord, nous appliquons la formule de multiplication abrégée "différence de carrés" et ouvrons les parenthèses intérieures.
(a^2+1)^2 - 4*a^2 = ((a^2+1)-2*a)*((a^2+1)+2*a) = (a^2+1 -2*a)*(a^2+1+2*a);
Notez que les expressions du carré de la somme et du carré de la différence de deux expressions sont obtenues entre parenthèses. Appliquez-les et obtenez la réponse.
a^2+1-2*a)*(a^2+1+2*a) = (a-1)^2*(a+1)^2 ;
Réponse:(a-1)^2*(a+1)^2 ;
Exemple 2
Factorisez le polynôme 4*x^2 - y^2 + 4*x +2*y.
Comme vous pouvez le voir directement ici, aucune des méthodes ne convient. Mais il y a deux carrés, ils peuvent être regroupés. Essayons.
4*x^2 - y^2 + 4*x +2*y = (4*x^2 - y^2) +(4*x +2*y) ;
Nous avons obtenu la formule de la différence des carrés dans la première tranche, et dans la deuxième tranche, il y a un facteur commun de deux. Appliquons la formule et supprimons le facteur commun.
(4*x^2 - y^2) +(4*x +2*y)= (2*x - y)*(2*x+y) +2*(2*x+y);
On voit que deux supports identiques sont obtenus. Nous les retirons comme un facteur commun.
(2*x - y)*(2*x+y) +2*(2*x+y) = (2*x+y)*(2*x - y)+2)= (2*x+ y )*(2*x-y+2);
Réponse:(2*x+y)*(2*x-y+2);
Comme vous pouvez le voir, il n'y a pas de méthode universelle. Avec l'expérience, la compétence viendra et la factorisation du polynôme en facteurs sera très facile.